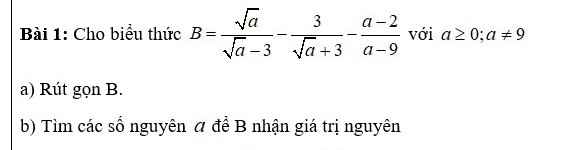a: Ta có: \(B=\dfrac{\sqrt{a}}{\sqrt{a}-3}-\dfrac{3}{\sqrt{a}+3}-\dfrac{a-2}{a-9}\)
\(=\dfrac{a+3\sqrt{a}-3\sqrt{a}+9-a+2}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}\)
\(=\dfrac{11}{a-9}\)
b: Để B nguyên thì \(11⋮a-9\)
\(\Leftrightarrow a-9=11\)
hay a=20
a) \(B=\dfrac{\sqrt{a}}{\sqrt{a}-3}-\dfrac{3}{\sqrt{a}+3}-\dfrac{a-2}{a-9}=\dfrac{\sqrt{a}\left(\sqrt{a}+3\right)-3\left(\sqrt{a}-3\right)-a+2}{a-9}=\dfrac{a+3\sqrt{a}-3\sqrt{a}+9-a+2}{a-9}=\dfrac{11}{a-9}\)
b) \(B\in Z\Leftrightarrow11⋮a-9\Leftrightarrow a-9\in\) Ư(11)\(=\left\{1;-1;11;-11\right\}\)
Mà \(a\ge0,a\ne9\)
\(\Rightarrow a\in\left\{10;8;20;\right\}\)(thỏa đk)