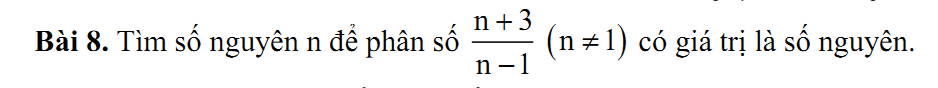Question

Answer 1

\(n\in Z\Rightarrow\dfrac{n+3}{n-1}\in Z\)

Để \(\dfrac{n+3}{n-1}\in Z\)

\(\Rightarrow\left(n+3\right)⋮\left(n-1\right)\\ \Rightarrow\left(n-1+4\right)⋮\left(n-1\right)\)

Vì \(\left(n-1\right)⋮\left(n-1\right)\)\(\Rightarrow4⋮\left(n-1\right)\Rightarrow n-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

Ta có bảng:

n-1	-1	1	-2	2	-4	4
n	0	2	-1	3	-3	5

Vậy \(n\in\left\{0;2;-1;3;-3;5\right\}\)

 

Answer 2

Để phân số \(\dfrac{n+3}{n-1}\) là số nguyên thì \(n+3⋮n-1\)

\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)

hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)