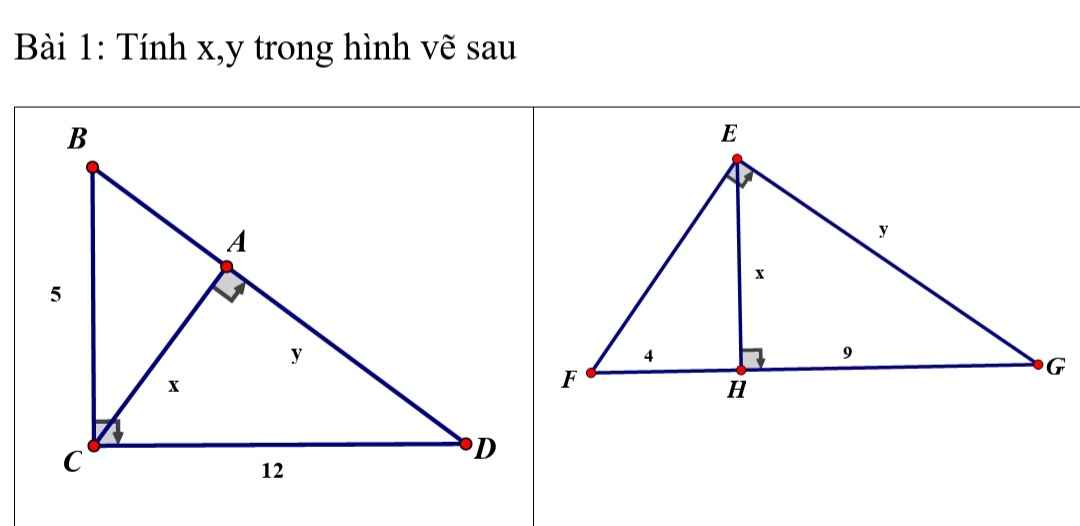
\(a,\) Xét \(\Delta BCD\) vuông tại \(C\), theo định lí PTG có:
\(BD=\sqrt{BC^2+CD^2}=\sqrt{5^2+12^2}=13\)
Áp dụng HTL trong tam giác vuông, ta được:
\(CD^2=AD\cdot BD\Leftrightarrow AD=y=\dfrac{CD^2}{BD}=\dfrac{12^2}{13}\approx11,1\)
Ta có \(AB+AD=BD\Leftrightarrow AB=13-11,1=1,9\)
Áp dụng HTL trong tam giác vuông, ta được:
\(AC^2=AB\cdot AD=21,09\Leftrightarrow AC=x\approx4,6\)
Vậy \(x\approx4,6\) ; \(y\approx11,1\)
Hình a:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBCD vuông tại C có CA là đường cao ứng với cạnh huyền BD, ta được:
\(\dfrac{1}{x^2}=\dfrac{1}{5^2}+\dfrac{1}{12^2}\)
\(\Leftrightarrow\dfrac{1}{x^2}=\dfrac{169}{3600}\)
hay \(x=\dfrac{60}{13}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔCAD vuông tại A, ta được:
\(y^2+\left(\dfrac{60}{13}\right)^2=12^2\)
\(\Leftrightarrow y=\dfrac{144}{13}\left(cm\right)\)