Lời giải:
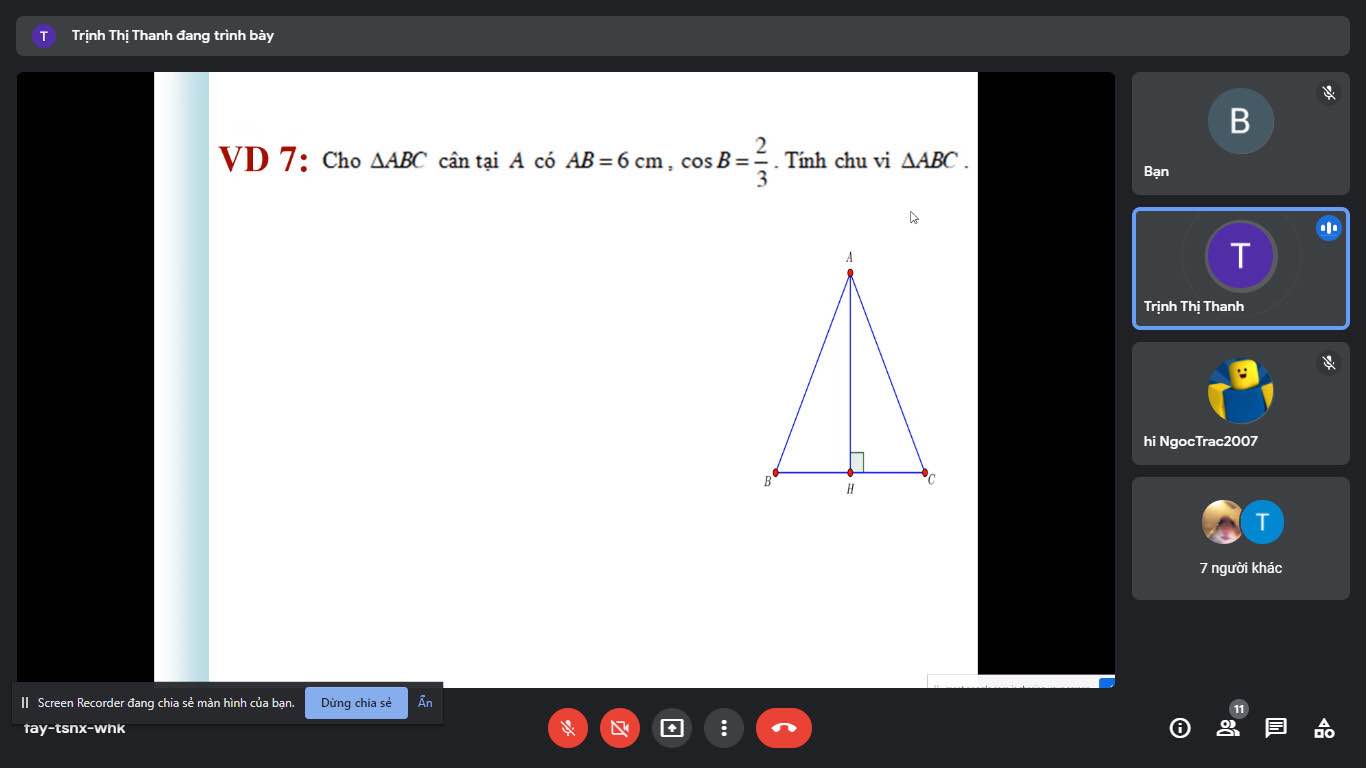
Kẻ $AH\perp BC$. Vì tam giác $ABC$ cân tại $A$ nên $AH$ đồng thời là đường trung tuyến.
$\Rightarrow 2BH=BC$
Xét tam giác $ABH$ vuông tại $H$:
$\frac{BH}{BA}=\cos B=\frac{2}{3}\Rightarrow BH=\frac{2}{3}BA=4$ (cm)
$BC=2BH=8$ (cm)
Chu vi tam giác $ABC$ là:
$AB+AC+BC=2AB+BC=2.6+8=20$ (cm)
tam giác ABC cân tại A \(\Rightarrow AB=AC=6\left(cm\right)\)
Ta có: \(cosB=\dfrac{2}{3}\Rightarrow\dfrac{BH}{AB}=\dfrac{2}{3}\Rightarrow BH=\dfrac{2}{3}.AB=\dfrac{2}{3}.6=4\left(cm\right)\)
tam giác ABC cân tại A có đường cao AH \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BC=2BH=4\left(cm\right)\)
\(\Rightarrow\) chu vi tam giác \(=AB+AC+BC=4+6+6=16\left(cm\right)\)