Cho tam giác ABC , góc A = 90 độ ; AB < AC , đường cao AH . Gọi D là điểm đối xứng của A qua H . Đường thẳng D // với AB cắt BC và AC lần lượt tại M và N .
a) Tứ giác ABDN là hình gì ? vì sao ?
b) Chứng minh : M là trực tâm của tam giác ACD
c) Gọi I là trung điểm của MC . Chứng minh : Góc HNI = 90 độ .
Vẽ hình ra hộ mình luôn nha ![]()
Bài 8: Đối xứng tâm
Cho tam giác ABC , góc A 90 độ ; AB AC , đường cao AH . Gọi D là điểm đối xứng của A qua H . Đường thẳng D // với AB cắt BC và AC lần lượt tại M và N .
a) Tứ giác ABDN là hình gì ? vì sao ?
b) Chứng minh : M là trực tâm của tam giác ACD
c) Gọi I là trung điểm của MC . Chứng minh : Góc HNI 90 độ .
Vẽ hình ra hộ mình luôn nha
Đọc tiếp
a: Xét tứ giác ABDN có AB//DN
nên ABDN là hình thang
mà \(\widehat{NAB}=90^0\)
nên ABDN là hình thang vuông
b: Ta có: DN//AB
AB\(\perp\)AC
Do đó: DN\(\perp\)AC
Xét ΔCAD có
CH là đường cao
DN là đường cao
CH cắt DN tại M
Do đó: M là trực tâm của ΔCAD
Đúng 0
Bình luận (0)
Cho góc xOy= 90 độ. Lấy điểm A nằm trong góc xOy. Lấy điểm B đối xứng với A qua Ox, điểm C đối xứng với A qua Oy. Chứng minh điểm B đối xứng với điểm C qua O.
nối góc O với góc A
Vì A đối xứng với C qua Oy=>Oy là đường trung trực của AC
=>OA=OC
=>Tam giác AOC cân tại O
Vì Oy là trung trực của AC nên Oy cũng là phân giác của O
=>O1=O2 1
Tương tự, ta có:
OA=OB,O3=O4 2
Từ 1 và 2 =>OC=OB 3
Góc AOC+AOB = 2(O2+O3)
=2.90o =180o
=>O,B,C thẳng hàng 4
Từ 3 và 4 =>B đối xứng với C qua O(đpcm)
xong![]()
Đúng 0
Bình luận (0)
cho hbh ABCD. đường chéo BD Kẻ AF\(\perp\)BD
a)CM: AE=CF
b)Tứ giác AECF là hình gì? Vì sao?
c) AF cắt CD tại I, CE cắt AB ở . CM: AK=CI
d)CM: AC,IK,DB đồng quy
Sửa đề; AE,CF vuông góc với BD
a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
c: Xét tứ giác AKCI có
AK//CI
AI//CK
Do đó: AKCI là hình bình hành
Suy ra: AK=CI
d: Ta có: AKCI là hình bình hành
nên Hai đường chéo AC và KI cắt nhau tại trung điểm của mỗi đường(1)
Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,IK,BD đồng quy
Đúng 0
Bình luận (0)
52/96Cho hình bình hành ABCD.Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. Chứng minh rằng điểm E đối xứng với điểm F qua điểm B.
53/96(sgk lớp 8 toán hình)
giải giúp nha
cảm ơn
bài 53 SGK
xét tứ giác AEMD có :
MD//AE (MD//AB)
ME//AD (ME//AC)
=> tứ giác AEMD là hình bành hành
=> AM,ED cắt nhau tại trung điểm mỗi đường
mà I là trung điểm của ED
=> I là trung điểm của AM
=> A,M đối xứng nhau qua I
Đúng 0
Bình luận (0)
93/92
Cho hình 14 trong đó DE//AB,DF//AC. Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.
giải giúp mk nha
92/91(sbt)hình lớp 8
giải giúp mk nha
Tứ giác ABCD là hình bình hành
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD (gt)
Suy ra: Tứ giác BMCD là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
AD // BC ( gt) hay DN // BC
Xét tứ giác BCND ta có:
DN // BC
DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) suy ra: M, C, N thẳng hàng và MC = CN
Vậy M và N đối xứng qua tâm C.
Đúng 0
Bình luận (0)
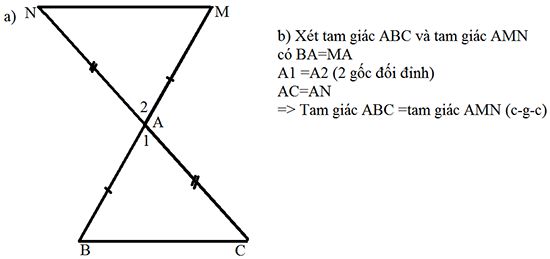
Vẽ tam giác ABC :
a) vẽ các điểm M, N tương ứng là đối xứng qua điểm A của các điểm B và C
b) 2 tam giác ABC và AMN có bằng nhau k? Vì sao?
Cho tam giác ABC .Dựng về phía ngoài các tam giác vuông cân tại A là tam giác ABD, tam giác ACE. Gọi AH là đường cao của tam giác ABC. Chứng minh AH đi qua trung điểm của DE.
B1: Cho hình bình hành ABCD. Trên đường chéo BD lấy 2 điểm E và F sao cho DE=BF.
a, C/m AECF là hình bình hành.
b, Gọi M và N lần lượt là giao điểm AE,CF với DC và AB. C/m AC,BD,MN đồng quy.
a: Xét ΔADE và ΔCBF có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
DE=BF
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Xét ΔABF và ΔCDE có
AB=CD
\(\widehat{ABF}=\widehat{CDE}\)
BF=DE
Do đó: ΔABF=ΔCDE
Suy ra: AF=CE
Xét tứ giác AECF có
AE=CF
AF=CE
Do đó: AECF là hình bình hành
b: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đo: AMCN là hình bình hành
Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường(1)
Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,MN đồng quy
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, vẽ điểm E thuộc AB, F thuộc CD sao cho AE=CF. Chứng minh rằng:
a, AECF là hình bình hành.
b, E, F đối xứng nhau qua tâm O của hình bình hành.
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Ta có: ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
hay O là trung điểm của AC
Ta có: AECF là hình bình hành
nên AC cắt FE tại trung điểm của mỗi đường
=>O là trung điểm của FE
hay F và E đối xứng nhau qua O
Đúng 0
Bình luận (0)