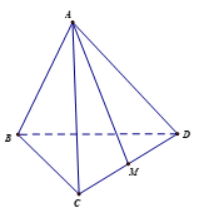
Cho tứ diện ABCD. Lấy G là trọng tâm của tam giác BCD. Khẳng định nào sau đây là sai?
A. \(\overrightarrow{BG}+\overrightarrow{CG}+\overrightarrow{DG}=\overrightarrow{0}\). B. \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}\).
C. \(\overrightarrow{BC}+\overrightarrow{BD}=3\overrightarrow{BG}\). D. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\).