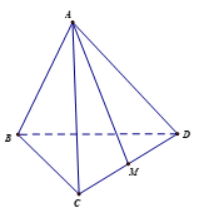
Tam giác ACD có ba cạnh bằng a nên tam giác ACD đều, AM là đường trung tuyến đồng thời là đường cao nên \(AM = \frac{{a\sqrt 3 }}{2}\).
Tam giác CBD có ba cạnh bằng a nên tam giác CBD đều, BM là đường trung tuyến đồng thời là đường cao nên \(BM = \frac{{a\sqrt 3 }}{2}\).
Áp dụng định côsin vào tam giác ABM ta có:
\(\cos \widehat {BAM} = \frac{{A{M^2} + A{B^2} - M{B^2}}}{{2AB.MB}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.a}} = \frac{{\sqrt 3 }}{3}\)
\(\overrightarrow {AB} .\overrightarrow {AM} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AM} } \right) = a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = \frac{{{a^2}}}{2}\)
Chọn B


