Question

Cho hình hộp ABCD.A’B’C’D’. Lấy M là trung điểm của đoạn thẳng CC’. Vectơ \(\overrightarrow{AM}\) bằng

A. \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}\).                          B. \(\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AA'}\).

C. \(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AA'}\).                   D. \(\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}\).

Answer 1

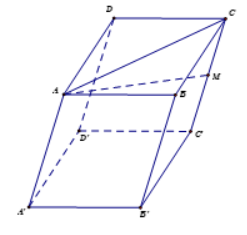
Vì M là trung điểm của CC’ nên \(\overrightarrow {AM}  = \frac{1}{2}\left( {\overrightarrow {AC'}  + \overrightarrow {AC} } \right) = \frac{1}{2}\left( {\overrightarrow {AA'}  + \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AB}  + \overrightarrow {AD} } \right)\)

\( = \frac{1}{2}\left( {\overrightarrow {AA'}  + 2\overrightarrow {AB}  + 2\overrightarrow {AD} } \right) = \frac{1}{2}\overrightarrow {AA'}  + \overrightarrow {AB}  + \overrightarrow {AD} \)

Chọn B.