Ý d ạ

Câu 4. Cho hàm số \( y = \frac{x^2 + bx + c}{x + n} \) có đồ thị và hai đường tiệm cận \( d_1, d_2 \) như hình vẽ dưới đây.
a) Hàm số đồng biến trên khoảng \( (0; +\infty) \).
b) Đồ thị hàm số có tiệm cận đứng là \( x = -1 \).
c) Điểm \( M(50; 98) \) và hai điểm cực trị của đồ thị hàm số thẳng hàng.
d) Đồ thị hàm số có một trục đối xứng là đường thẳng \( y = (p + \sqrt{q})(x + 1) - r \) (trong đó \( p, q, r \) là các số nguyên). Khi đó \( p + 10q + 15r = 90 \).
Hai tiệm cận có pt là: \(x-y=0\) và \(x+1=0\)
Phương trình phân giác 2 tiệm cận có dạng:
\(\dfrac{\left|x-y\right|}{\sqrt{2}}=\dfrac{\left|x+1\right|}{1}\)
\(\Rightarrow\left[{}\begin{matrix}x-y=\sqrt{2}\left(x+1\right)\\y-x=\sqrt{2}\left(x+1\right)\end{matrix}\right.\)
\(\Rightarrow y=\left(1+\sqrt{2}\right)\left(x+1\right)-1\)








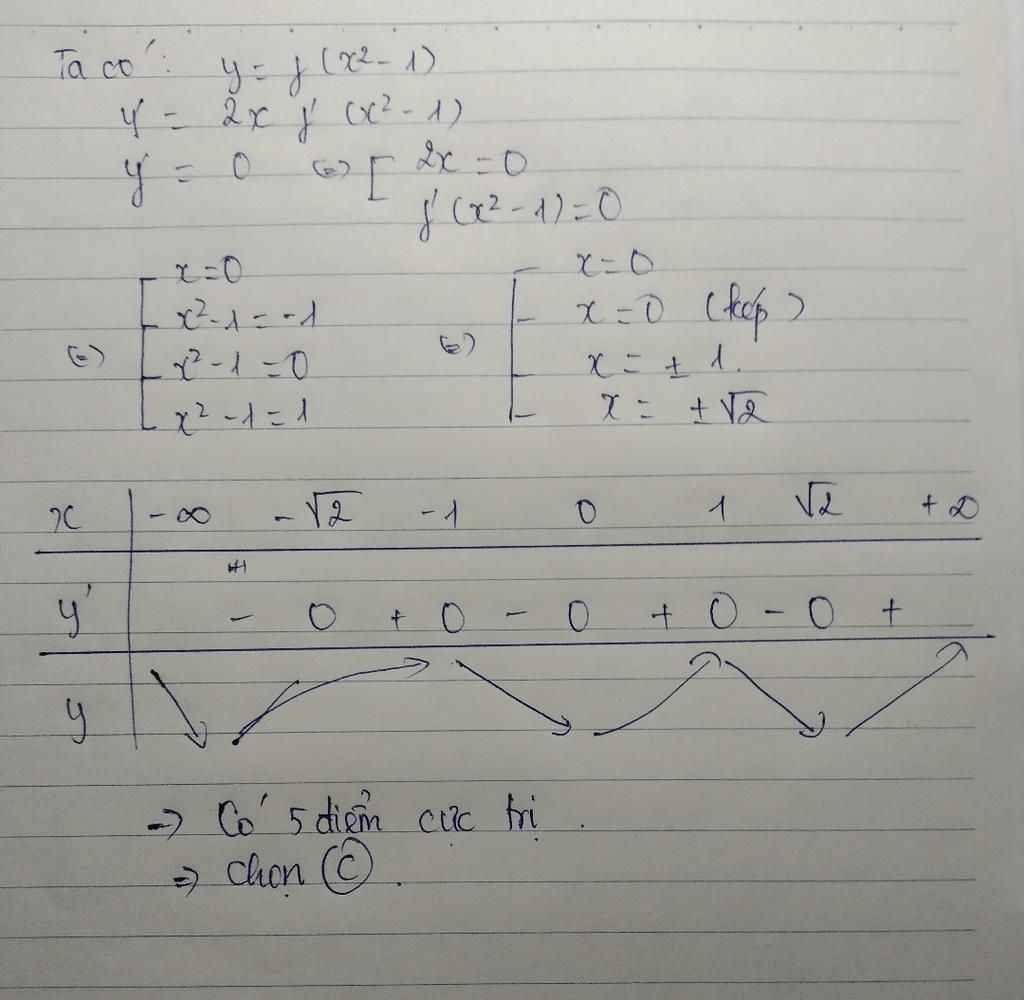

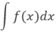 bằng:
bằng: