Các câu hỏi tương tự
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = x 2 trên đoạn [-3; 0];
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].
Cho hàm số y
-
x
2
+
2
n
ế
u
-
2
≤
x
≤...
Đọc tiếp
Cho hàm số y =
-
x
2
+
2
n
ế
u
-
2
≤
x
≤
1
x
n
ế
u
1
<
x
≤
3
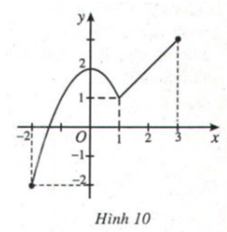
Có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.
Cho hàm số
y
x
+
1
x
-
1
. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m A. -6 B.
2
3
C.
3
2
D.
6
5
Đọc tiếp
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
+
3
-
x
ln
x
trên đoạn [1;2] là: A. B. C. D.
Đọc tiếp
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + 3 - x ln x trên đoạn [1;2] là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y f(x) nghịch biến trên
ℝ
và thỏa mãn [f(x) - x]f(x)
x
6
+
3
x
4
+
2
x
2
,
∀
x
∈
ℝ
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng A. 4 B. -28 C. -3 D. 33
Đọc tiếp
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Kí hiệu M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
x
2
+
x
+
4
x
+
1
trên đoạn [0;3]. Tính giá trị của
M
m
.
Đọc tiếp
Kí hiệu M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của M m .
![]()
![]()
![]()
![]()
Giá trị nhỏ nhất của hàm số
y
x
-
1
x
+
1
trên đoạn [0; 3] là: A.
m
i
n
0
;
3
-
3
B.
m
i...
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = x - 1 x + 1 trên đoạn [0; 3] là:
A. m i n 0 ; 3 = - 3
B. m i n 0 ; 3 = 1 2
C. m i n 0 ; 3 = - 1
D. m i n 0 ; 3 = 1
Giá trị nhỏ nhất của hàm số
y
x
-
1
x
+
1
trên đoạn [0; 3] là: A.
m
i
n
0
;
3
y
-
3
B.
m...
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = x - 1 x + 1 trên đoạn [0; 3] là:
A. m i n 0 ; 3 y = - 3
B. m i n 0 ; 3 y = 1 2
C. m i n 0 ; 3 y = - 1
D. m i n 0 ; 3 y = 1


