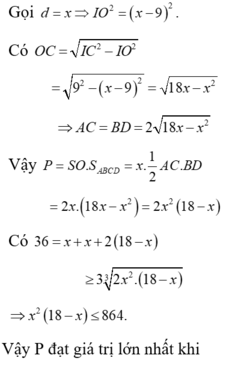Các câu hỏi tương tự
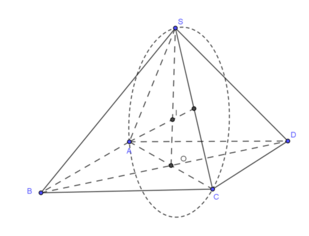
Xét hình chóp từ giác đều S.ABCD có tam giác SAC nội tiếp trong đường tròn có bán kính bằng 9. Gọi d là khoảng cách từ S đến mặt phẳng (ABCD) và T là diện tích tứ giác ABCD. Tính d khi biểu thức
P
d
.
T
đạt giá trị lớn nhất. A.
d
10
B.
d
17
C.
d
15
D.
d
12
Đọc tiếp
Xét hình chóp từ giác đều S.ABCD có tam giác SAC nội tiếp trong đường tròn có bán kính bằng 9. Gọi d là khoảng cách từ S đến mặt phẳng (ABCD) và T là diện tích tứ giác ABCD. Tính d khi biểu thức P = d . T đạt giá trị lớn nhất.
A. d = 10
B. d = 17
C. d = 15
D. d = 12
Cho chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a và tam giác SAD đều đồng thời nằm trong mặt phẳng vuông góc đáy. Tính khoảng cách d từ tâm đường tròn nội tiếp tam giác SAD đến mặt phẳng
S
B
C
theo a A.
d
2
a
21
7
B.
d
4
a...
Đọc tiếp
Cho chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a và tam giác SAD đều đồng thời nằm trong mặt phẳng vuông góc đáy. Tính khoảng cách d từ tâm đường tròn nội tiếp tam giác SAD đến mặt phẳng S B C theo a
A. d = 2 a 21 7
B. d = 4 a 57 57
C. d = 2 a 21 21
D. d = 4 a 21 21
Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D, có AB 2AD 2CD , tam giác SAD đều và nằm trong mặt phẳng vuông góc đáy. Gọi I là trung điểm AD, biết khoảng cách từ I đến mặt phẳng (SBC) bằng 1(cm). Tính diện tích S hình thang ABCD. A.
S
10
3
c
m
2
B.
S
20...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D, có AB = 2AD = 2CD , tam giác SAD đều và nằm trong mặt phẳng vuông góc đáy. Gọi I là trung điểm AD, biết khoảng cách từ I đến mặt phẳng (SBC) bằng 1(cm). Tính diện tích S hình thang ABCD.
A. S = 10 3 c m 2
B. S = 20 3 c m 2
C. S = 200 27 c m 2
D. S = 5 3 c m 2
Cho mặt cầu
S
có bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
C
có chu vi bằng
8
π
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn
C
, điểm D thuộc
S
(D không thuộc đường tròn
C
) và tam giác ABC là...
Đọc tiếp
Cho mặt cầu S có bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu S theo giao tuyến là đường tròn C có chu vi bằng 8 π . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn C , điểm D thuộc S (D không thuộc đường tròn C ) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu (S) bán kính
R
5
c
m
. Mặt phẳng
P
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
cm
. Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5 c m . Mặt phẳng P cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π cm . Bốn điểm A, B, C, D thay đổi sao A, B, C cho thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB a; AD 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC) A.
d
a
1315
89
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB = a; AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = 2 a 1315 89
C. d = 2 a 1513 89
D. d = a 1513 89
Cho mặt cầu (S) bán kính R 5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
.
B. ...
Đọc tiếp
Cho mặt cầu (S) bán kính R = 5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3 .
B. 60 3 c m 3 .
C. 20 3 c m 3 .
D. 96 3 c m 3 .
Cho hình chóp S.ABCD có đáy là hình chữ nhật,
A
B
a
,
A
D
2
a
.
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
45
°
.Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC). A.
d
a
1315...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a , A D = 2 a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 ° .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC).
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuống tại A và D có
A
B
2
A
D
2
C
D
.
Tam giác SAD đều và nằm trong mặt phẳng vuống góc với đáy. Gọi I là trung điểm AD. Biết khoảng cách từ I đến mặt phẳng (SBD) bằng 1cm Tính diện tích hình thang ABCD. A.
S
200
27
c
m...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuống tại A và D có A B = 2 A D = 2 C D . Tam giác SAD đều và nằm trong mặt phẳng vuống góc với đáy. Gọi I là trung điểm AD. Biết khoảng cách từ I đến mặt phẳng (SBD) bằng 1cm Tính diện tích hình thang ABCD.
A. S = 200 27 c m 2
B. S = 10 3 c m 2
C. S = 5 3 c m 2
D. S = 19 2 c m 2