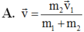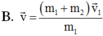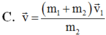Xét hai vật được coi là hai chất điểm có khối lượng m1 và m2 chuyển động trên một đường thẳng nằm ngang không ma sát đến va chạm với nhau. Gọi v → 1 , v → 1 / , v → 2 , v → 2 / là vecto vận tốc của các vật trước và sau va chạm, v → 1 , v → 1 / , v → 2 , v → 2 / là các giá trị đại số của chúng. Chứng minh rằng v 1 / , v 2 / xác định bằng các biểu thức: v 1 / = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 ; v 2 / = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2
Theo tính chất của và chạm thì: v → 1 ≠ v → 1 / , v → 2 ≠ v → 2 /
Theo phương ngang động lượng của hệ được bảo toàn nên ta có:
m 1 v 1 / + m 2 v 2 / = m 1 v 1 + m 2 v 2 (1)
Động năng của hệ được bảo toàn:
m 1 v 1 / 2 2 + m 2 v 2 / 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 (2)
Từ (1) ⇒ m 1 ( v 1 − v 1 / ) = m 2 ( v 2 / − v 2 ) (3)
Từ (2) ⇒ m 1 ( v 1 2 − v 1 / 2 ) = m 2 ( v 2 / 2 − v 2 2 ) (4)
Chia (4) cho (3) vế theo vế ta được: v 1 + v 1 / = v 2 / + v 2 (5)
Từ (5) ⇒ v 2 / = v 1 + v 1 / − v 2 (6)
Thay (6) vào (3) ta được:
v 1 / = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 ; v 2 / = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2