Các câu hỏi tương tự
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn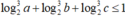 
. Khi biểu thức 
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
cho các số thực dương a,b,c thỏa mãn a+b+c=ab+bc+ac. Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{a^2}{a^2+3bc}+\frac{b^2}{b^2+3ac}+\frac{c^2}{c^2+3ab}+\sqrt{a+b+c}\)
cho 3 số thực dương a,b,c. Tìm giá trị nhỏ nhất của:
\(\)\(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{4}{\sqrt{a^2+b^2+c^2+1}}\)
Cho các số dương a, b, c thỏa mãn a,b,c Giá trị lớn nhất của biểu thức Pcosb+cosc-
4
sin
3
a
2
là A.
4
6
B.
2
3
6
C.
4
3...
Đọc tiếp
Cho các số dương a, b, c thỏa mãn a,b,c Giá trị lớn nhất của biểu thức P=cosb+cosc- 4 sin 3 a 2 là
A. 4 6
B. 2 3 6
C. 4 3 6
D. 1 6
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
a,b,c thuộc[0;1] tìm giá trị lớn nhất S=a(1-b)+b(1-c)+c(1-a)
Giả sử a,b,c ,d lập thành một cấp số nhân. Tính giá trị biểu thức
(
a
-
c
)
2
+
(
b
-
c
)
2
+
(
b
-
d
)
2
-
(
a
-
d...
Đọc tiếp
Giả sử a,b,c ,d lập thành một cấp số nhân. Tính giá trị biểu thức ( a - c ) 2 + ( b - c ) 2 + ( b - d ) 2 - ( a - d ) 2
A. 3
B. 2
C. 1
D. 0
Cho 3 số thực a,b,c. Tìm giá trị nhỏ nhất của biểu thức:
\(S=\frac{1344}{a+\sqrt{ab}+\sqrt[3]{abc}}-\frac{2016}{\sqrt{a+b+c}}\)