Các câu hỏi tương tự
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
tính giá trị biểu thức saua) Adfrac{9^4}{3^2}b) B81.left(dfrac{5}{3}right)^4c) Cleft(dfrac{4}{7}right)^{-4}.left(dfrac{2}{7}right)^3d) D7^{-6}.left(dfrac{2}{3}right)^0.left(dfrac{7}{5}right)^6e) E8^3:left(dfrac{2}{3}right)^5.left(dfrac{1}{3}right)^2f) Fleft(dfrac{7}{9}right)^{-2}.left(dfrac{1}{sqrt{3}}right)^8g) Gleft(dfrac{-4}{5}right)^{-2}.left(dfrac{2}{5}right)^2.left(sqrt{2}right)^3
Đọc tiếp
tính giá trị biểu thức sau
a) \(A=\dfrac{9^4}{3^2}\)
b) \(B=81.\left(\dfrac{5}{3}\right)^4\)
c) \(C=\left(\dfrac{4}{7}\right)^{-4}.\left(\dfrac{2}{7}\right)^3\)
d) \(D=7^{-6}.\left(\dfrac{2}{3}\right)^0.\left(\dfrac{7}{5}\right)^6\)
e) \(E=8^3:\left(\dfrac{2}{3}\right)^5.\left(\dfrac{1}{3}\right)^2\)
f) \(F=\left(\dfrac{7}{9}\right)^{-2}.\left(\dfrac{1}{\sqrt{3}}\right)^8\)
g) \(G=\left(\dfrac{-4}{5}\right)^{-2}.\left(\dfrac{2}{5}\right)^2.\left(\sqrt{2}\right)^3\)
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn 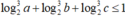 . Khi biểu thức
. Khi biểu thức ![]()
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
cho các số thực dương a,b,c thỏa mãn a+b+c=ab+bc+ac. Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{a^2}{a^2+3bc}+\frac{b^2}{b^2+3ac}+\frac{c^2}{c^2+3ab}+\sqrt{a+b+c}\)
cho ba số thực dương a,b,c thỏa mãn \(a^2+b^2+c^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{a^3}{2b+3c}+\dfrac{b^3}{2c+3a}+\dfrac{c^3}{2a+3b}\)
Câu 6: Cho góc a thỏa cos alpha = 4/5 và 0 < alpha < pi/2 Giá trị cia * sin 2alpha bằng A. - 12/25 B. 24/25 C. - 24/25 D. 12/25
tính giá trị biểu thức saua) Adfrac{25^6}{5^3}b) B32.left(dfrac{3}{2}right)^5c) Cleft(dfrac{1}{3}right)^4.3^{-3}d) D4^{-2}.left(dfrac{2}{5}right)^5.5^4e) E9^{-5}:left(dfrac{5}{3}right)^4.25^2f) Fleft(dfrac{5}{8}right)^{-2}:4^2g) Gleft(dfrac{5}{3}right)^3.left(dfrac{9}{2}right)^2:left(sqrt{3}right)^4
Đọc tiếp
tính giá trị biểu thức sau
a) \(A=\dfrac{25^6}{5^3}\)
b) \(B=32.\left(\dfrac{3}{2}\right)^5\)
c) \(C=\left(\dfrac{1}{3}\right)^4.3^{-3}\)
d) \(D=4^{-2}.\left(\dfrac{2}{5}\right)^5.5^4\)
e) \(E=9^{-5}:\left(\dfrac{5}{3}\right)^4.25^2\)
f) \(F=\left(\dfrac{5}{8}\right)^{-2}:4^2\)
g) \(G=\left(\dfrac{5}{3}\right)^3.\left(\dfrac{9}{2}\right)^2:\left(\sqrt{3}\right)^4\)
Gieo một con súc sắc hai lần.
a. Mô tả không gian mẫu
b. Phát biểu các biến cố sau dưới dạng mệnh đề:
A: = {(6,1), (6,2), (6,3), (6,4), (6, 5), (6, 6)}
B: = {(2, 6), (6, 2), (3, 5), (5, 3), (4, 4), (1, 7), (7, 1)}
C: = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}.










