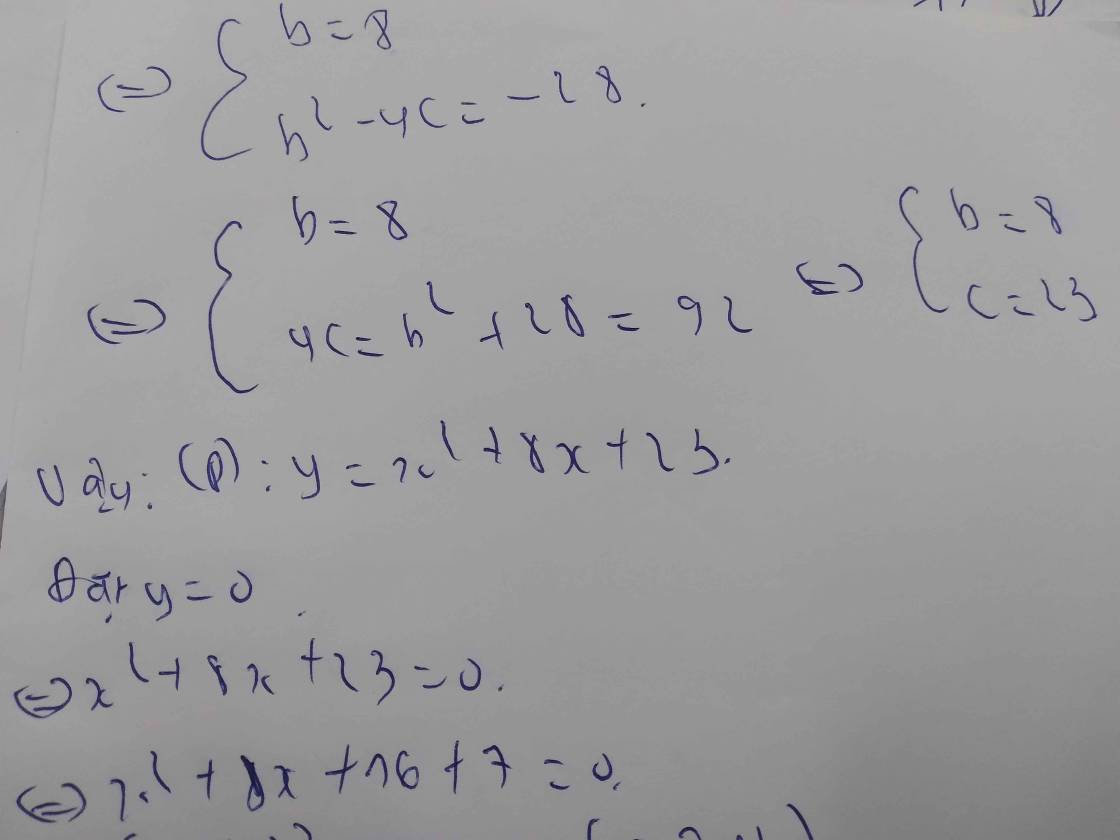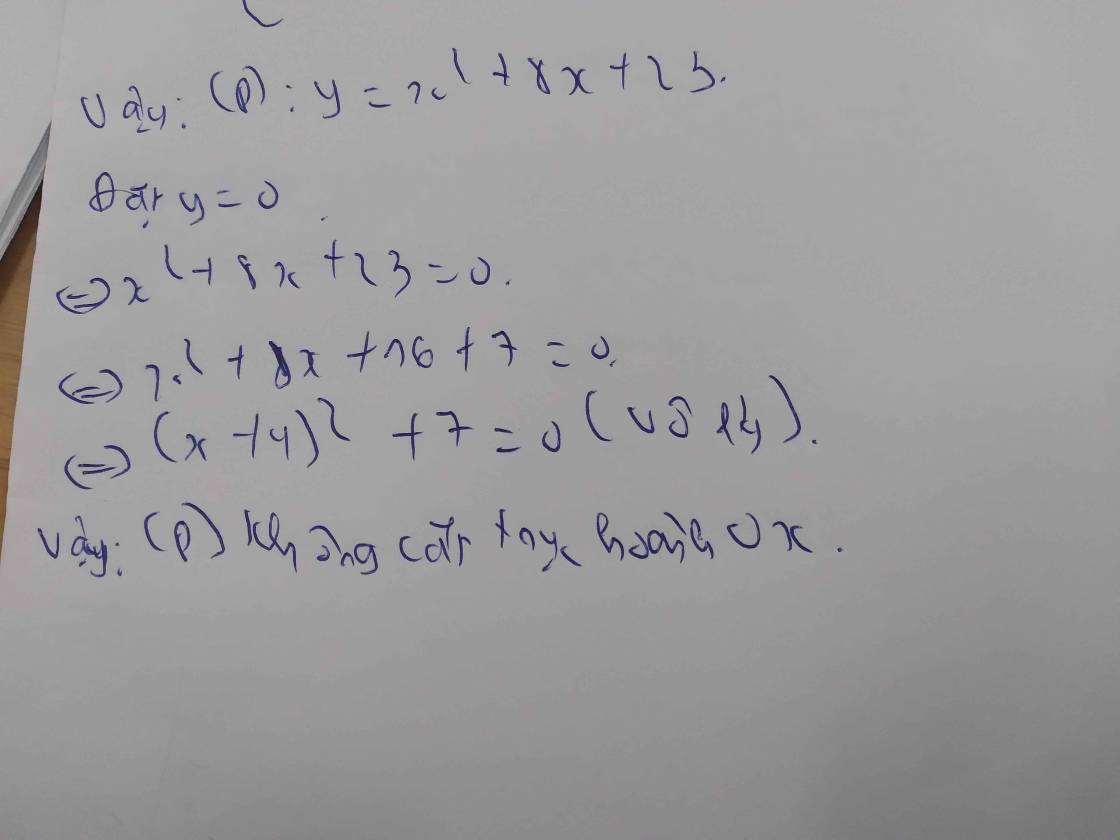Các câu hỏi tương tự
Xác định tọa độ đỉnh, phương trình của trục đối xứng của parabol y = ax2 + bx + c.
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của một parabol: y = x2 - 2x
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của một parabol: y = -x2 + 4
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của một parabol: y = x2 - 3x + 2
Xác định parabol (P): y a
x
2
+ bx + c, biết rằng (P) cắt trục Ox tại hai điểm có hoành độ lần lượt là −1 và 2, cắt trục Oy tại điểm có tung độ bằng −2. A. Y −2
x
2
+ x − 2. B. Y −
x
2
+ x − 2. C. Y
1
2
x
2
+ x − 2. D. Y...
Đọc tiếp
Xác định parabol (P): y = a x 2 + bx + c, biết rằng (P) cắt trục Ox tại hai điểm có hoành độ lần lượt là −1 và 2, cắt trục Oy tại điểm có tung độ bằng −2.
A. Y = −2 x 2 + x − 2.
B. Y = − x 2 + x − 2.
C. Y = 1 2 x 2 + x − 2.
D. Y = x 2 – x − 2.
Xác định tọa độ giao điểm của parabol y = ax2 + bx + c với trục tung. Tìm điều kiện để parabol này cắt trục hoành tại hai điểm phân biệt, tại mỗi điểm và viết tọa độ của các giao điểm trong mỗi trường hợp.
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của một parabol:
a) y = x2 - 3x + 2 ; b) y = -2x2 + 4x - 3;
c) y = x2 - 2x ; d) y = -x2 + 4.
Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của một parabol: y = -2x2 + 4x - 3
Cho hàm số y=x²-2-3x,đồ thị là parabol(P) a/Xác định tọa độ đỉnh,trục đối xứng.Lập bảng biến thiên và vẽ đồ thị b/gọi A là điểm thuộc(P) và có hoành độ bằng 5. Tìm phương trình đường thẳng (d) đi qua 2 điểm A,I