Đáp án B
Cách1: Tư duy tự luận
Hàm số liên tục tại điểm x = 1 khi lim x → 1 f x = f 1 .
Ta có f 1 = k và lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 .
= lim x → 1 x 2016 − x + 2 x − 1 2018 x + 1 + x + 2018 2018 x + 1 − x + 2018 2018 x + 1 + x + 2018
= lim x → 1 x x − 1 x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 x − 1
= lim x → 1 x x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 = 2015 + 2 .2 1019 2017
= 2 2019
Vậy để hàm số liên tục tại điểm x=1 khi k = 2 2019
Cách 2: Tư duy tự luận (tính giới hạn bằng công thức L’Hospital)
Ta có
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = lim x → 1 2016 x 2015 + 1 1009 2018 x + 1 − 1 2 x + 2018
= 2016 + 1 1009 2019 − 1 2 2019 = 2 2019
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Cách 3: Sử dụng máy tính cầm tay (casio và vinacal)
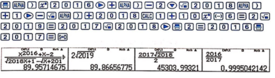
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = 2 2019 .
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .




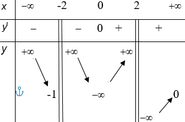
 Xét các khẳng định sau:
Xét các khẳng định sau: