Ta có (C) có tâm I(m; 0) và bán kính R= 3 nên theo đề bài ta được:
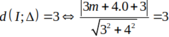
![]()
m= 4 và m= -6
Chọn B.
Ta có (C) có tâm I(m; 0) và bán kính R= 3 nên theo đề bài ta được:
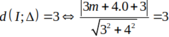
![]()
m= 4 và m= -6
Chọn B.
Với những giá trị nào của m thì đường thẳng ∆: 4x+ 3y + m= 0 tiếp xúc với đường tròn (C): x2+ y2- 9= 0.
A. m= -3
B. m= 3 và m= -3
C. m= 3
D. m= 15 và m= -15
Cho đường tròn (C): x 2 + y 2 + 4 x − 4 y − 10 = 0 và đường thẳng ∆: x + y + m = 0. Giá trị m để đường thẳng tiếp xúc với đường tròn là:
A. m = ± 6
B. m = ± 3
C. m = ± 8
D.Không tồn tại m
Cho đường thẳng Δ: x + 2y + m = 0 và đường tròn (C): x 2 + y 2 = 9. Giá trị của m để Δ tiếp xúc với (C) là:
A. m = 3 5
B. m = - 3 5
C. m = ± 3 5
D. m = 5
Với giá trị nào của m thì đường thẳng Δ:3x– y+ 2m=0 tiếp xúc với đường tròn (C): x²+ y²+ 6x– 2y=0
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
Cho đường tròn (C): x 2 + y 2 + 8 x + 6 y + 5 = 0 và đường thẳng ∆: 3x – 4y + m = 0. Giá trị của m để đường thẳng cắt đường tròn theo dây cung dài nhất là
A. m = 0
B. m = 2
C. m = 4
D. m = 6
Cho đường tròn (C): x 2 + y 2 - 4 x + 2 y + 1 = 0 . Để qua điểm A(m+2; 1) kẻ được hai tiếp tuyến với đường tròn (C) và hai tiếp tuyến tạo với nhau một góc 120° thì giá trị m là:
A. m = ± 2 2
B. m = ± 2 3
C. m = ± 2 3 3
D. Không tồn tại giá trị của m
Cho đường tròn (C) có phương trình x 2 + y 2 + 4 x + 2 y + 4 = 0 . Để qua điểm A(m; 2 – m) có hai tiếp tuyến với (C) và hai tiếp tuyến đó tạo với nhau góc 60 ° thì m nhận giá trị là
A. m = 0
B. m = ± 1
C. m = ± 2
D. Không tồn tại m
cho đường tròn (C) : (x-2)^2+(y+1)^2=25 xác định m để đường thẳng (d) : 3x-4y+m=0 là tiếp tuyến của (C)