Các câu hỏi tương tự
Với a,b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x 3 + a x 2 - b x + 1 là
A. 2.
B. 0.
C. 3.
D. 1.
Với a,b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x 3 + a x 2 - b x + 1 là
A. 2.
B. 0.
C. 3.
D. 1.
Với a, b là hai số thực dương bất kì. Số điểm cực trị của hàm số y = x3 + ax2 – bx + 1 là
A. 2
B. 1
C. 0
D. 3
Cho hàm số
y
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tập tất cả các giá trị của m để đồ thị hàm số
y
f
x
có 5 điểm cực trị là...
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
2
x
3
-
3
(
m
+
1
)
x
2
+
6
m
x
có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng
d
:
y
x
+
2
Số phần tử của S là A. 0 B. 1 C...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Cho hàm số
y
f
(
x
)
có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của hàm số
y
f
(
x
)
là – 2, 0, 2, a , 6 với 4 a 6. Số điểm cực trị của hàm số
y
f
(
x
6
−
3
x
2
)
là A. 8 B. 11 C. 9 D. 7
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
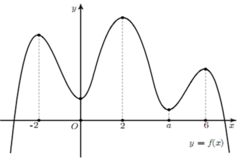
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Cho hàm số bậc ba
y
ax
3
+
bx
2
+
cx
+
d
có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số
y
|
ax...
Đọc tiếp
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số y = | ax 2 | x | + bx 2 + c | x | + d | là
A. 5
B. 7
C. 9
D. 11
Cho hàm số yf(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn [a;b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn[a,b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;...
Đọc tiếp
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3




