Question

 

vẽ hình

Answer 1

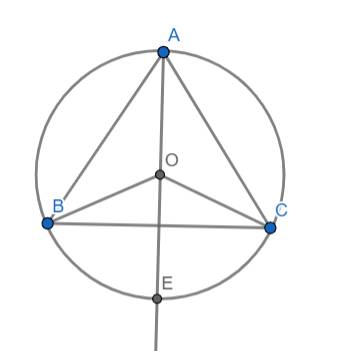
a) Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó 

⇒ O ∈ đường trung trực của tam giác ABC 

Mà ΔABC cân tại A 

⇒ AO là đường trung trực của tam giác ABC 

⇒ AO ⊥ BC hay AE ⊥ BC 

⇒ E nằm chính giữa cung nhỏ BC

Hay: \(\text{sđ}\stackrel\frown{BE}=\text{sđ}\stackrel\frown{CE}\) 

Mà: \(\text{sđ}\stackrel\frown{BC}=\text{sđ}\stackrel\frown{BE}+\text{sđ}\stackrel\frown{CE}\)

\(\Rightarrow\text{sđ}\stackrel\frown{BE}=\text{sđ}\stackrel\frown{CE}=\dfrac{100^o}{2}=50^o\) 

\(\Rightarrow\left\{{}\begin{matrix}\widehat{BOE}=\text{sđ}\stackrel\frown{BE}=50^o\\\widehat{COE}=\text{sđ}\stackrel\frown{CE}=50^o\end{matrix}\right.\)

b) Ta có: \(\widehat{AOB}+\widehat{BOE}=180^o\) (kề bù) 

\(\Rightarrow\widehat{AOB}=180^o-50^o=130^o\)

Mà: \(\widehat{AOB}=\text{sđ}\stackrel\frown{AB}=130^o\)  

Do ΔABC cân tại A \(\Rightarrow AB=AC\) 

\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}=130^o\)