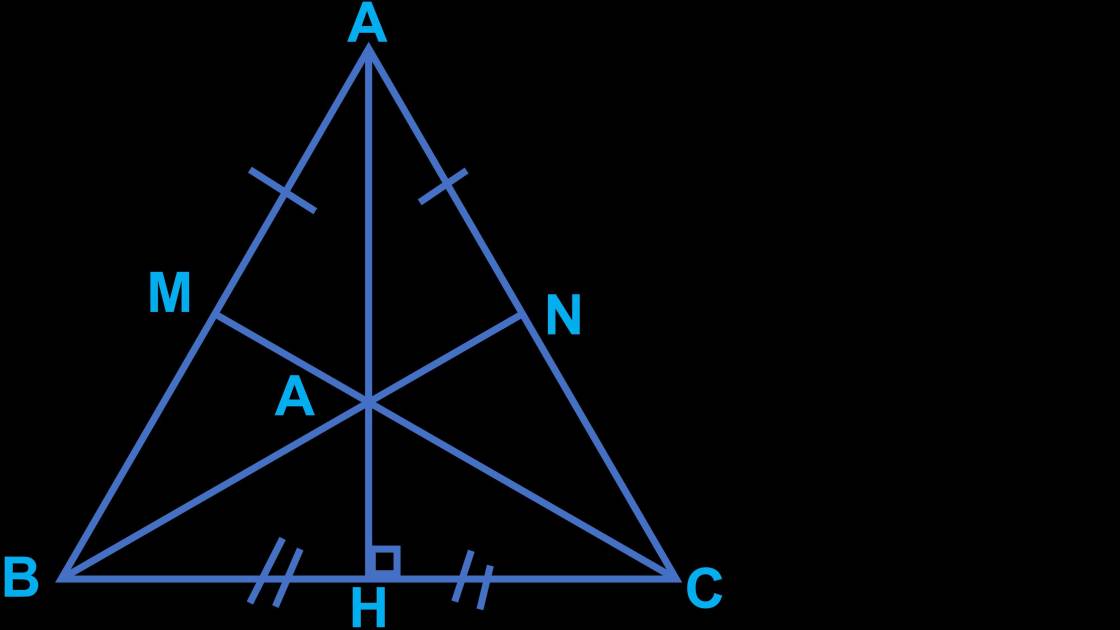
câu 22 : a) xét ΔABN và ΔACM, ta có :
AB = AC (vì ΔABC cân tại A)
góc A là góc chung
AM = AN (gt)
⇒ ΔABN = ΔACM (c.g.c)
b) ta có : MA + MB = AB
và NA + NC = AC
mà AM = AN và AB = AC
=> MB = AB - MA (1)
=> NC = AC - NA (2)
từ (1) và (2) ⇒ MB = NC
vì ΔABN = ΔACM nên ⇒ BN = CM (2 cạnh tương ứng)
xét ΔMIB và ΔNIC, ta có :
MB = NC (cmt)
\(\widehat{MIB}=\widehat{NIC}\) (đối đỉnh)
BN = CM (cmt)
⇒ ΔMIB = ΔNIC (c.g.c)
vì ΔMIB = ΔNIC nên ⇒ IM = IN (2 cạnh tương ứng)
xét ΔAIM và ΔAIN, ta có :
AM = AN (gt)
AI là cạnh chung
IM = IN (cmt)
⇒ ΔAIM = ΔAIN (c.c.c)
⇒ \(\widehat{MAI}=\widehat{NAI}\) (2 góc tương ứng)
⇒ AI là tia phân giác của \(\widehat{A}\)
c) gọi H là giao điểm của AI và BC
xét ΔAHB và ΔAHC, ta có :
AB = AC (vì ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\) (câu b)
AH là cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)
⇒ \(\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứg) (3)
⇒ HB = HC (2 cạnh tương ứng) (4)
từ (3) và (4) ⇒ AH là đường trung trực của BC
⇒ AI là đường trung trực của BC
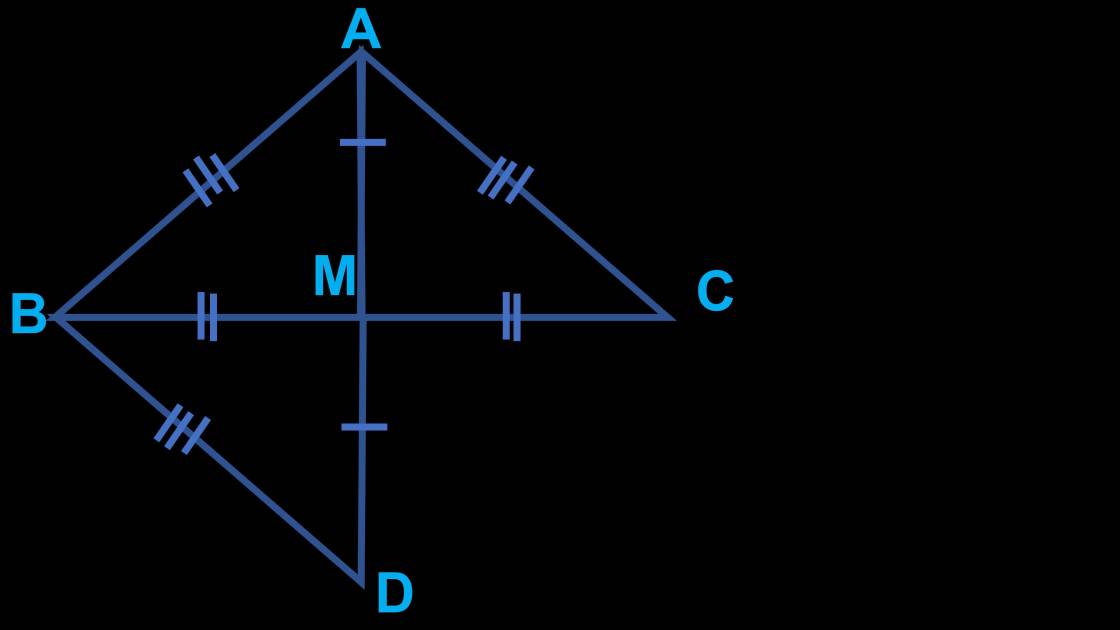
câu 23 : a) xét ΔABM và ΔACM, ta có :
AB = AC (vì ΔABC cân tại A)
MB = MC (vì M là trung điểm của BC)
AM là cạnh chung
⇒ ΔABM và ΔACM (c.c.c)
b) xét ΔBMD và ΔCMA, ta có :
MB = MC (vì M là trung điểm của BC)
\(\widehat{BMD}=\widehat{CMA}\) (đối đỉnh)
MD = MA (gt)
⇒ ΔBMD = ΔCMA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
đây là hình vẽ của từng câu nha :
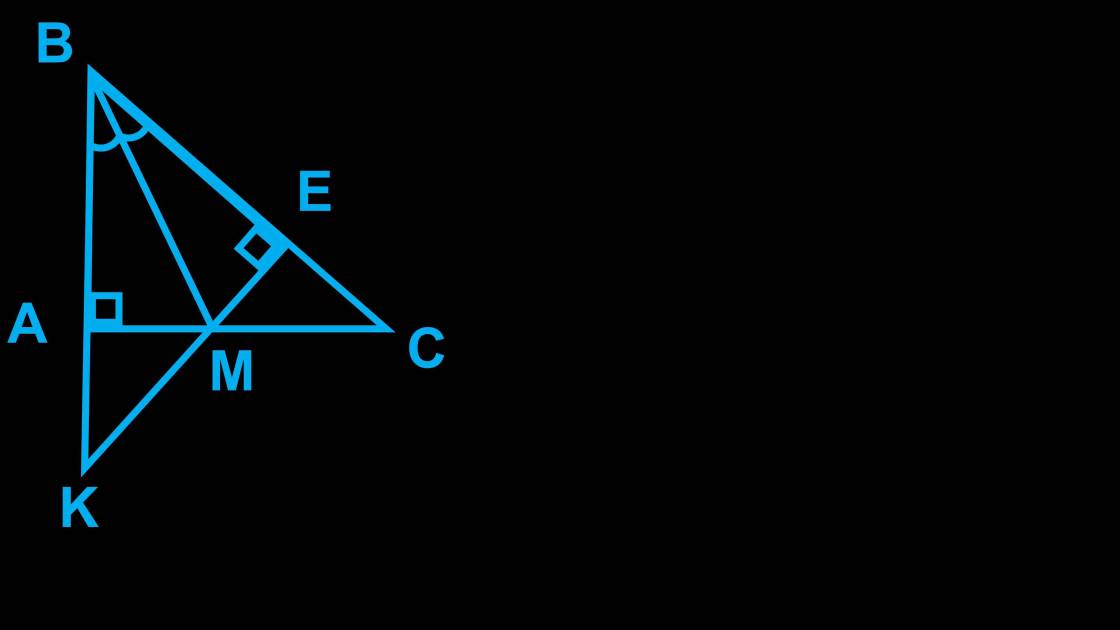
câu 21 :
câu 22 :
câu 23 :