Bài 3:
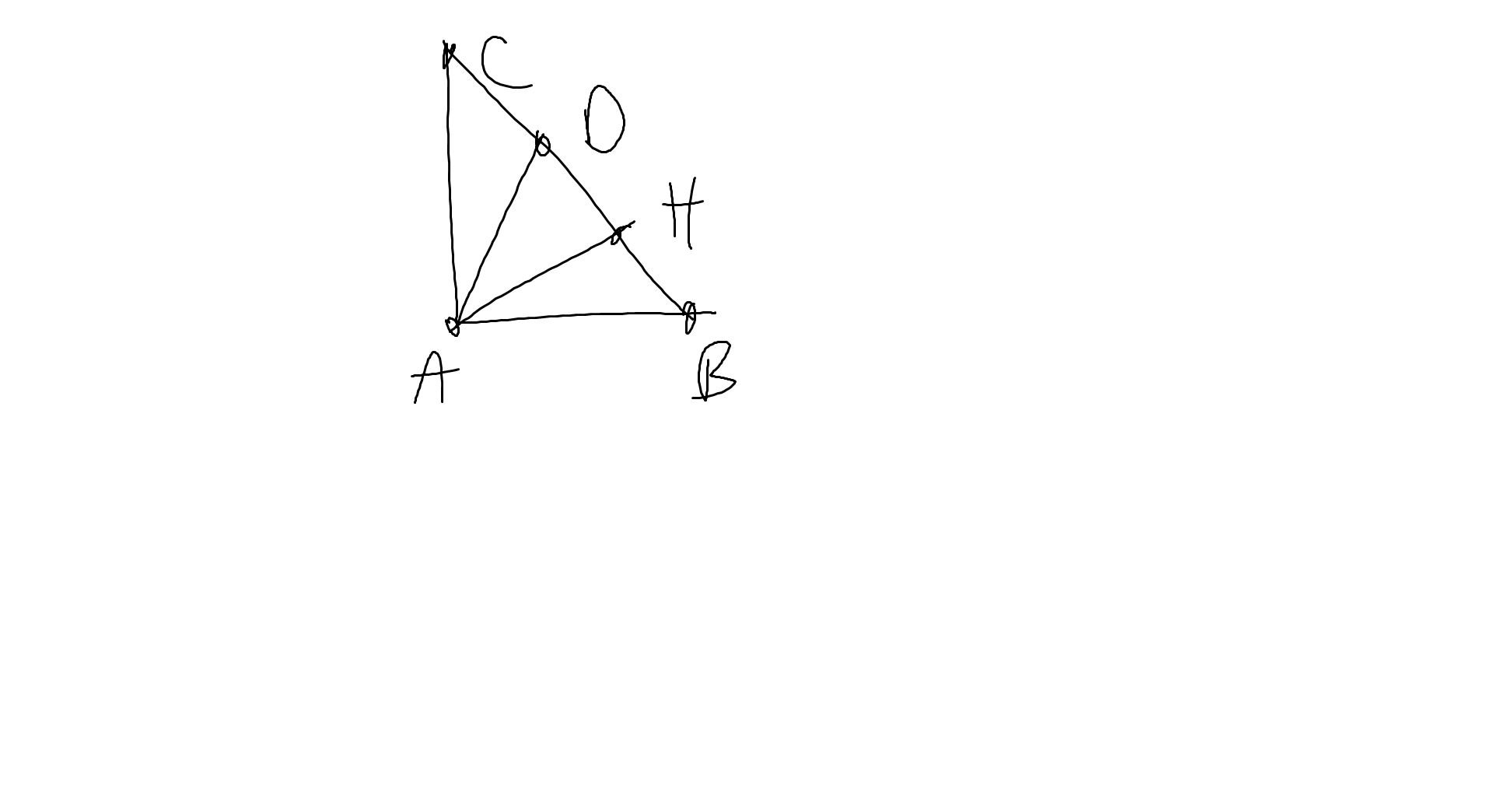
Ta có: \(\widehat{BAD}+\widehat{DAC}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{DAC}=\widehat{HAD}\)(AD là phân giác của góc HAC)
nên \(\widehat{BAD}=\widehat{BDA}\)
Xét ΔBAD có \(\widehat{BAD}=\widehat{BDA}\)
nên ΔBAD cân tại B
Xét ΔBAD cân tại B có \(\widehat{ABD}=60^0\)
nên ΔBAD đều
=>\(\widehat{BAD}=\widehat{BDA}=\widehat{ABD}\)
Bài 4:
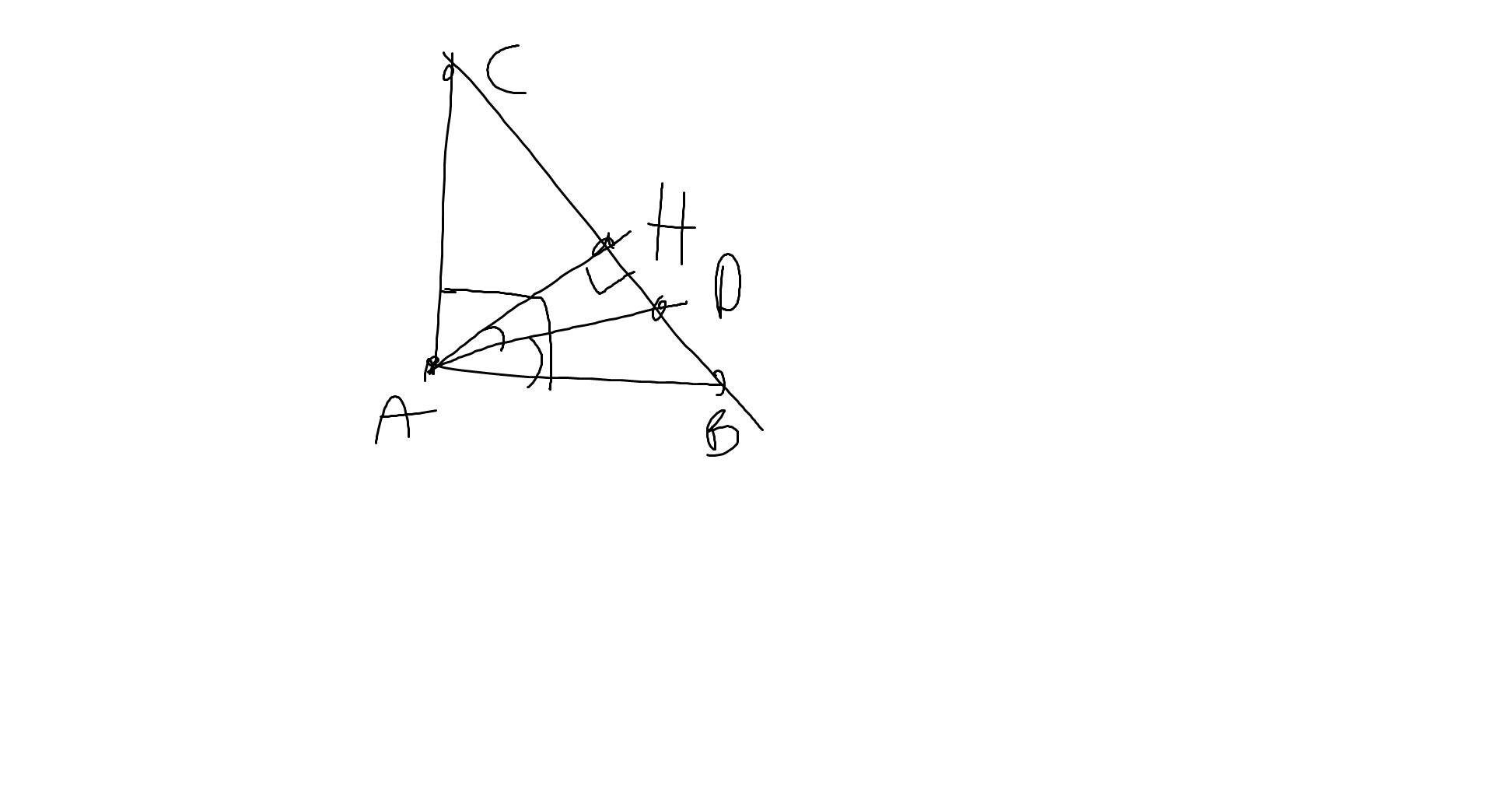
a: Ta có: \(\widehat{ABH}+\widehat{HAB}=90^0\)(ΔHAB vuông tại H)
\(\widehat{HAC}+\widehat{HAB}=\widehat{BAC}=90^0\)
Do đó: \(\widehat{ABH}=\widehat{HAC}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{CAB}=90^0\)
\(\widehat{CDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác của góc BAH)
nên \(\widehat{CAD}=\widehat{CDA}\)

 Vẽ hình + giải
Vẽ hình + giải