Question

 vẽ hình có gt /kl

Answer 1

a: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

=>PA\(\perp\)BD tại A

Xét (O) có

ΔCIB nội tiếp

CB là đường kính

Do đó: ΔCIB vuông tại I

Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)

nên ADHC là tứ giác nội tiếp

b: Xét ΔDBP có

PA,BH là các đường cao

PA cắt BH tại C

Do đó: C là trực tâm của ΔDBP

=>DC\(\perp\)BP

mà CI\(\perp\)BP

mà DC,CI có điểm chung là C

nên D,C,I thẳng hàng

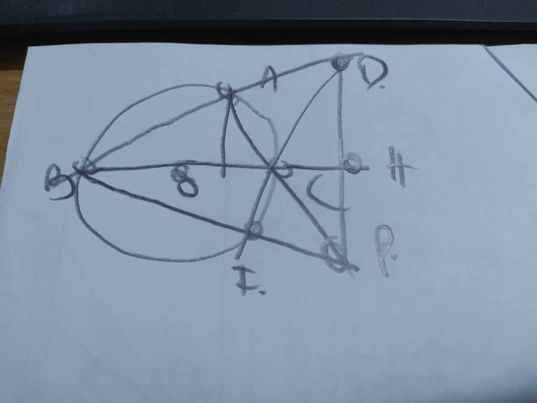
GT	(O) có đường kính BC \(A\in\left(O\right);AP>AC;P\in AC\) PB\(\cap\)(O)={I} PH\(\perp\)BC tại H, PH cắt BA tại D
KL	a: ACHD nội tiếp b: D,C,I thẳng hàng