Bài 3:
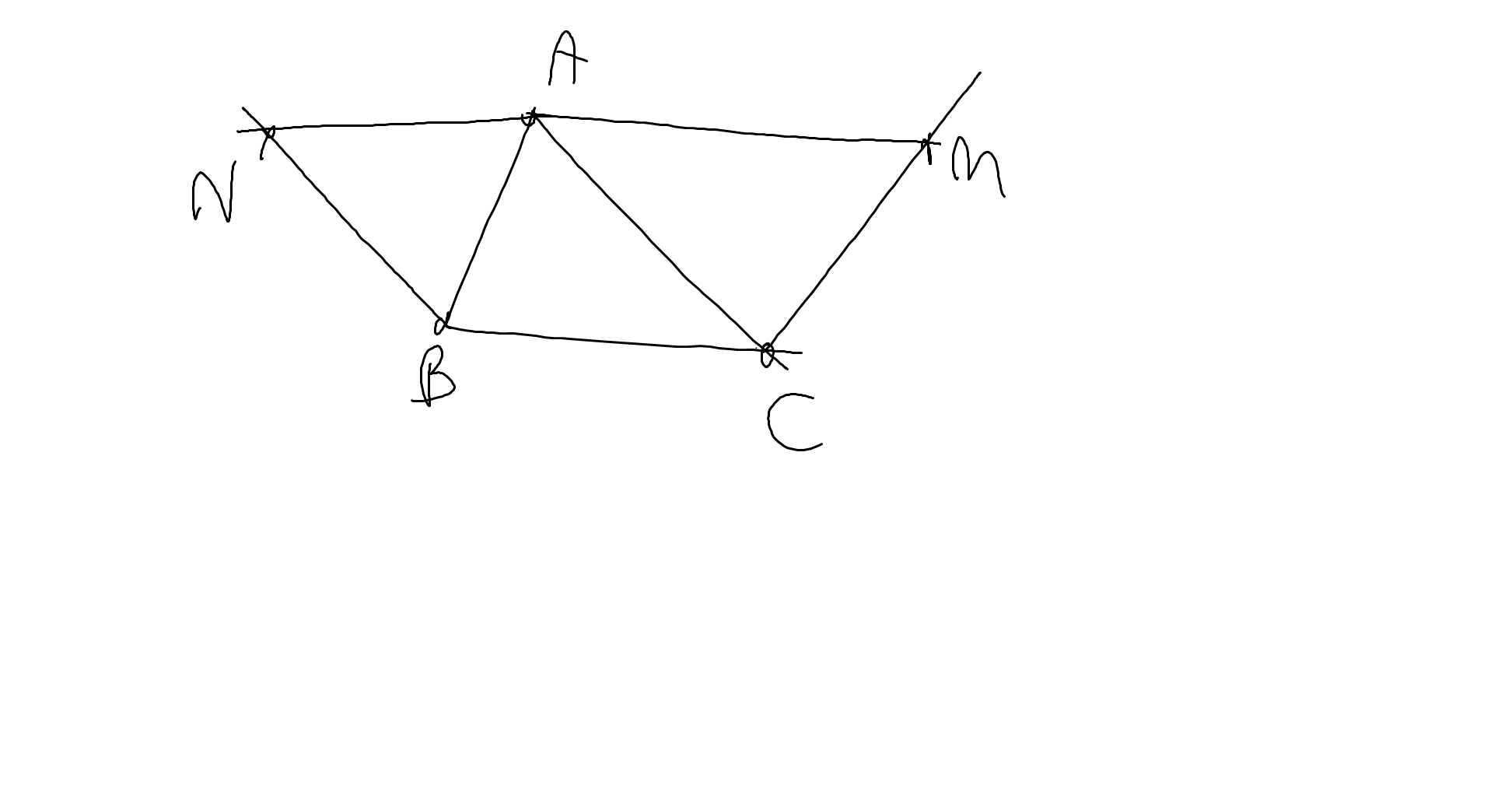
a: Xét ΔBAM và ΔABC có
\(\widehat{BAM}=\widehat{ABC}\)(hai góc so le trong, AM//BC)
AB chung
\(\widehat{BMA}=\widehat{CAB}\)(hai góc so le trong, CA//BM)
Do đó: ΔBAM=ΔABC
Xét ΔNAC và ΔBCA có
\(\widehat{NAC}=\widehat{BCA}\)(hai góc so le trong, NA//BC)
AC chung
\(\widehat{NCA}=\widehat{BAC}\)(hai góc so le trong, CN//AB)
Do đó: ΔNAC=ΔBCA
b: ΔBAM=ΔABC
=>AM=BC
ΔNAC=ΔBCA
=>NA=BC
mà MA=BC
nên MA=NA
Ta có: M,A,N thẳng hàng
mà MA=NA
nên A là trung điểm của MN
Bài 4:
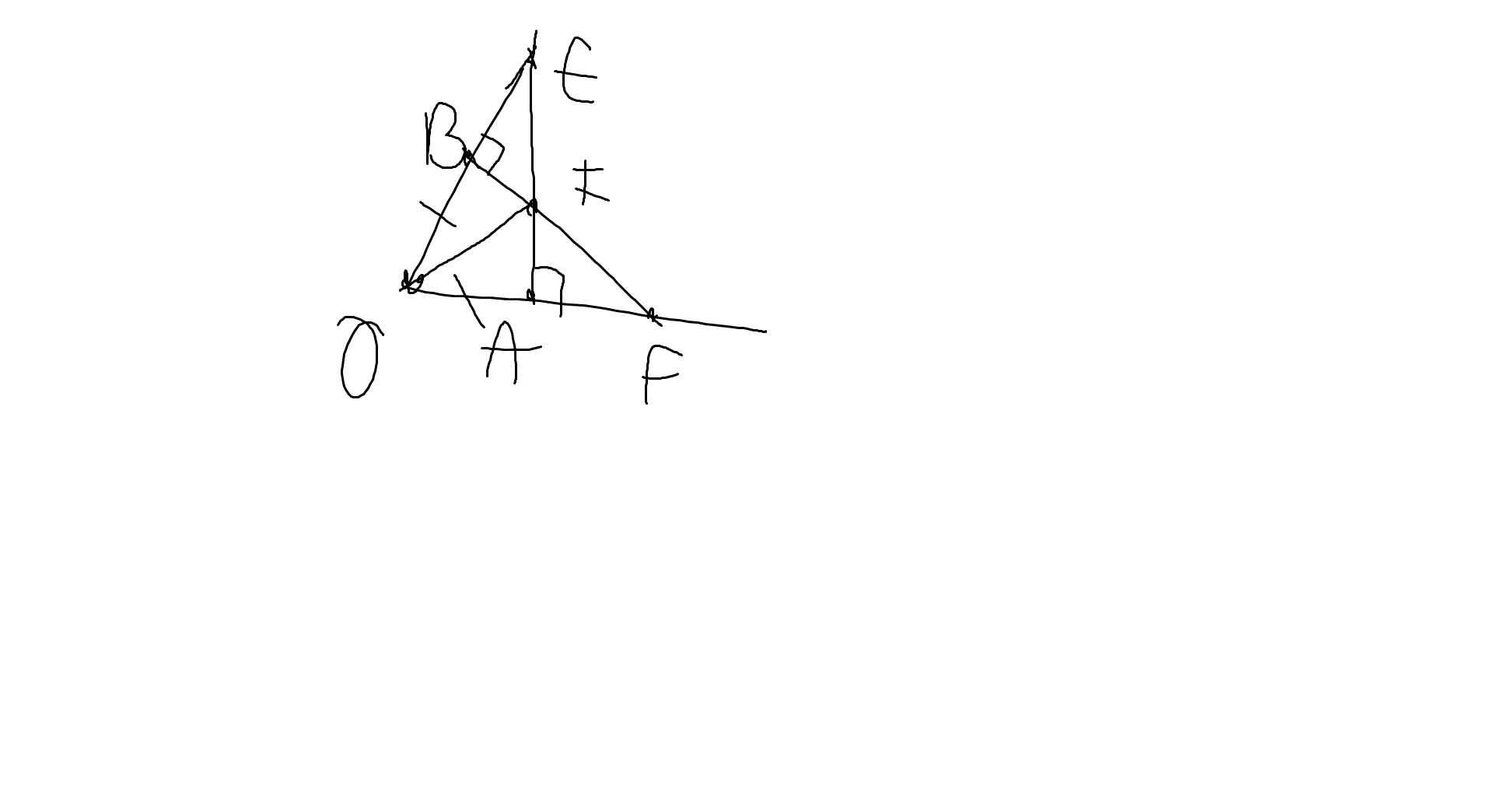
a: Xét ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
\(\widehat{AOE}\) chung
Do đó: ΔOAE=ΔOBF
=>AE=BF
b: ΔOAE=ΔOBF
=>\(\widehat{OEA}=\widehat{OFB}\) và OE=OF
Ta có: OA+AF=OF
OB+BE=OE
mà OA=OB và OF=OE
nên AF=BE
Xét ΔIAF vuông tại A và ΔIBE vuông tại B có
AF=BE
\(\widehat{IFA}=\widehat{IEB}\)
Do đó: ΔIAF=ΔIBE
c: ΔIAF=ΔIBE
=>IA=IB
Xét ΔOAI vuông tại A và ΔOBI vuông tại B có
OI chung
IA=IB
Do đó: ΔOAI=ΔOBI
=>\(\widehat{AOI}=\widehat{BOI}\)
=>OI là phân giác của góc AOB

 ve + giai
ve + giai











