ve + giai
Bài 1:
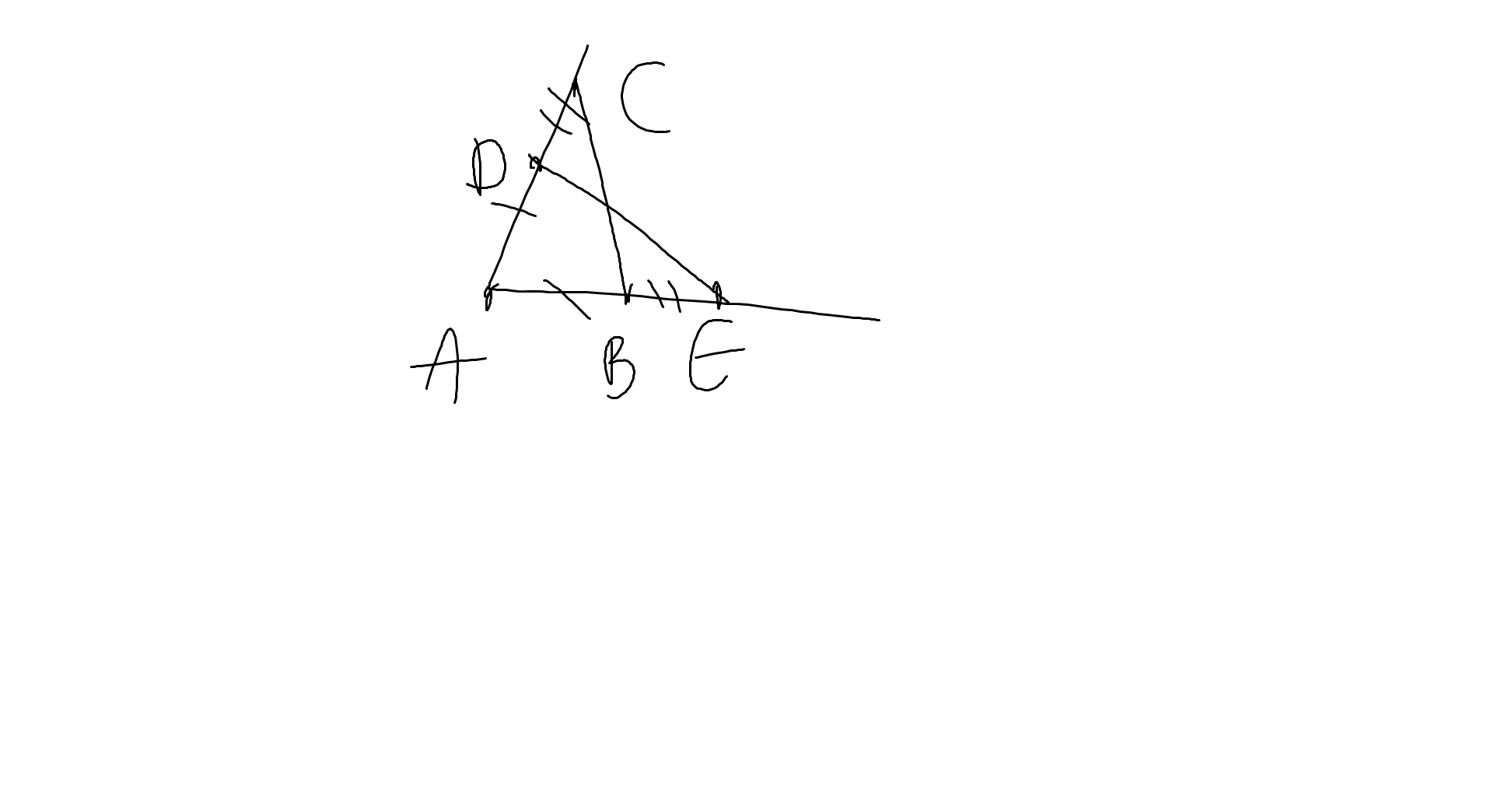
Ta có: AE=AB+BE
AC=AD+DC
mà AB=AD và BE=DC
nên AE=AC
Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}\) chung
AC=AE
Do đó: ΔABC=ΔADE
Bài 2:
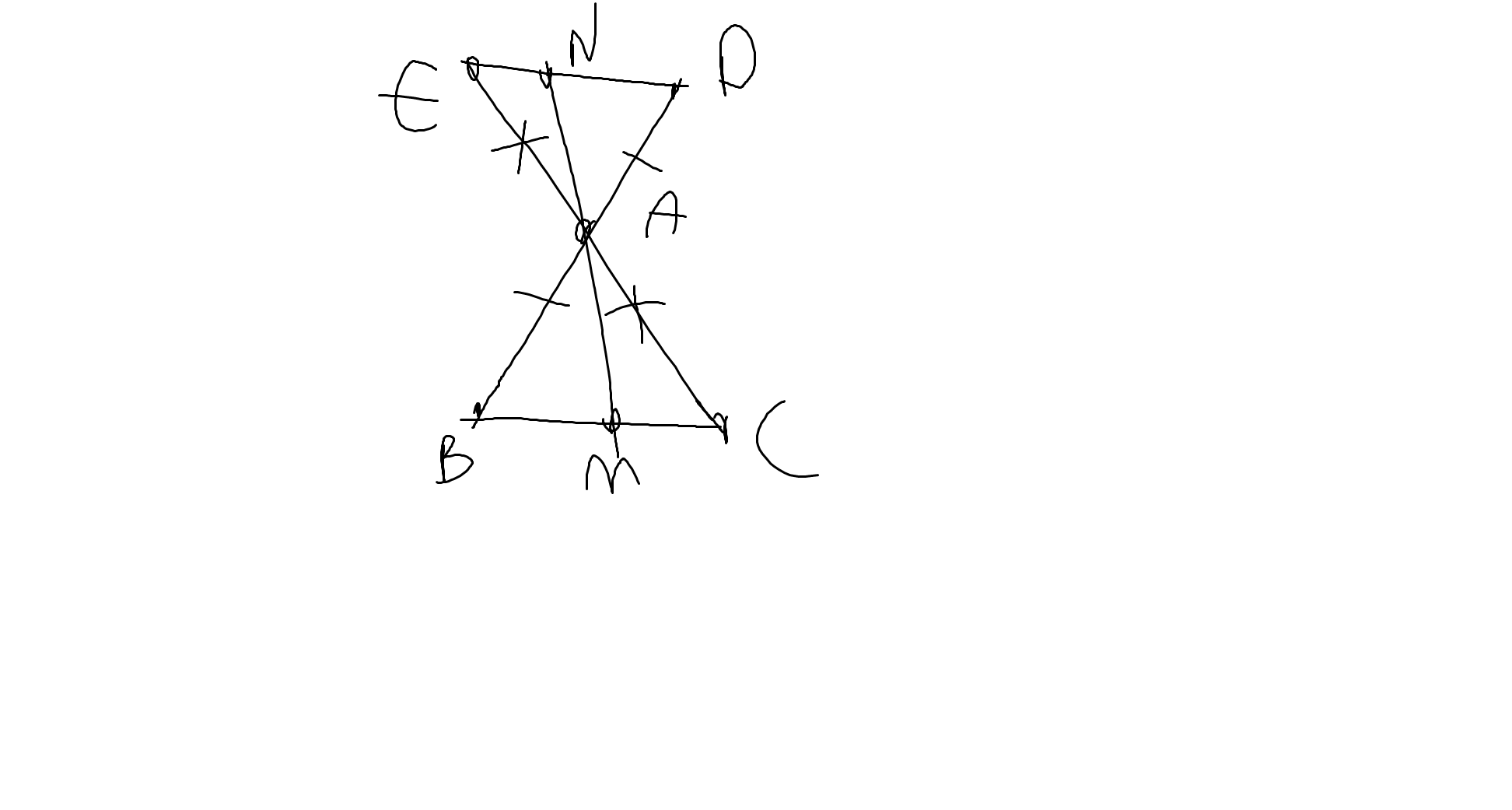
a: Xét ΔADE và ΔABC có
AD=AB
\(\widehat{DAE}=\widehat{BAC}\)(hai góc đối đỉnh)
AE=AC
Do đó ΔADE=ΔABC
=>\(\widehat{ADE}=\widehat{ABC};\widehat{AED}=\widehat{ACB}\)
b: Xét ΔAEN và ΔACM có
\(\widehat{AEN}=\widehat{ACM}\)(cmt)
AE=AC
\(\widehat{EAN}=\widehat{CAM}\)(hai góc đối đỉnh)
Do đó: ΔAEN=ΔACM
=>AN=AM
Đúng 1
Bình luận (0)
