Đặt f(x) = x 2 , x ∈ R
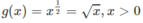
Đồ thị:
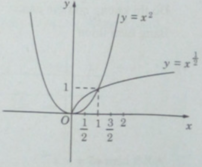
Từ đồ thị của hai hình đó ta có:
f(0,5) < g(0,5);
f(1) = g(1) = 1;
f(3/2) > g(3/2), f(2) > g(2);
f(3) > g(3), f(4) > g(4).
Đặt f(x) = x 2 , x ∈ R
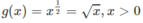
Đồ thị:

Từ đồ thị của hai hình đó ta có:
f(0,5) < g(0,5);
f(1) = g(1) = 1;
f(3/2) > g(3/2), f(2) > g(2);
f(3) > g(3), f(4) > g(4).
Vẽ đồ thị của các hàm số y = x 2 và y = x 1 2 trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi x = 0,5; 1; 3/2; 2; 3; 4.
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x 2 , y = x 1 2 , y = x - 1
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x - 1 x + 1 và các trục tọa độ. Khi đó giá trị của S bằng
A. S = ln2 - 1 (đvdt)
B. S = 2ln2 - 1 (đvdt)
C. S = 2ln2 + 1 (đvdt)
D. S = ln2 + 1 (đvdt)
Gọi S là diện tích hình phẳng giưới hạn bởi đồ thị của hàm số (H): y = x - 1 x + 1 và các trục tọa độ. Khi đó giá trị của S bằng
A. 2ln2 + 1
B. ln2 + 1
C. ln2 - 1
D. 2ln2 - 1
Trên hình 2.13, đồ thị của ba hàm số y = ax, y = bx, y = cx (a, b, c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c
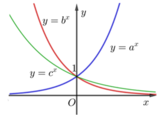
![]()
![]()
![]()
![]()
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
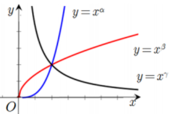
Cho các hàm số y = x α , y = x β , y = x γ có đồ thị trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào dưới đây đúng
![]()
![]()
![]()
![]()
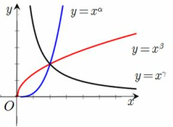
Cho các hàm số y = x α ; y = x β ; y = x γ có đồ thị trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào dưới đây đúng.
![]()
![]()
![]()
![]()