Question

Vẽ đồ thị các hàm số sau đây a) y = x ^ 2 - 3x + 4 b) y = - x ^ 2 + 2x + 3 Giúp mk vs

Answer 1

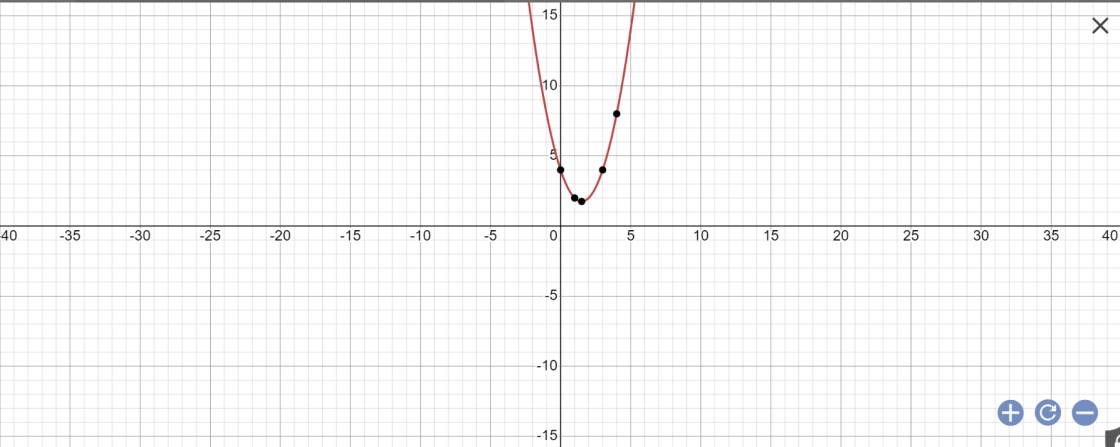
a: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-3\right)}{2}=\dfrac{3}{2}\\y=-\dfrac{\left(-3\right)^2-4\cdot1\cdot4}{4\cdot1}=-\dfrac{9-16}{4}=\dfrac{7}{4}\end{matrix}\right.\)

Vì \(y=x^2-3x+4\) có a=1>0

nên hàm số sẽ đồng biến khi \(x>\dfrac{3}{2}\) và nghịch biến khi \(x< \dfrac{3}{2}\)

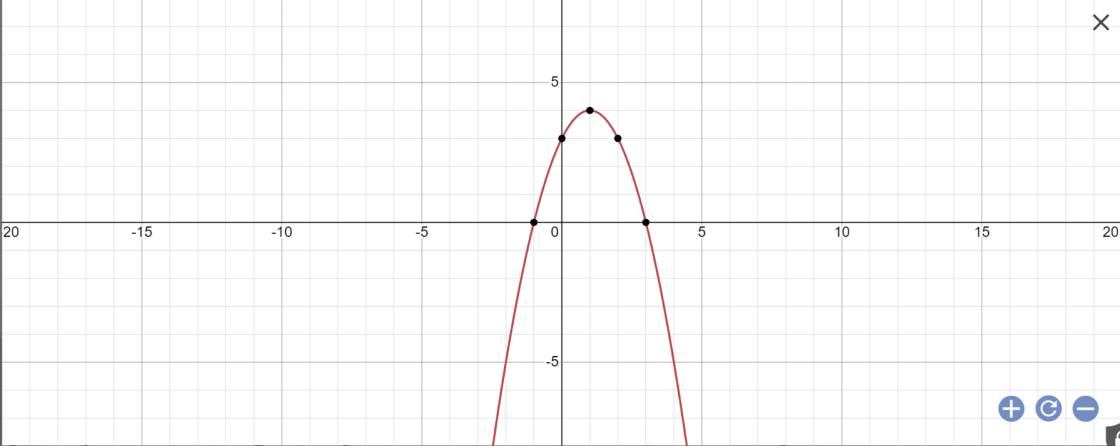
b: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=-\dfrac{2}{2\cdot\left(-1\right)}=\dfrac{-2}{-2}=1\\y=-\dfrac{2^2-4\cdot\left(-1\right)\cdot3}{4\cdot\left(-1\right)}=-\dfrac{4+12}{-4}=4\end{matrix}\right.\)

Vì \(y=-x^2+2x+3\) có a=-1<0

nên hàm số đồng biến khi x<1 và nghịch biến khi x>1