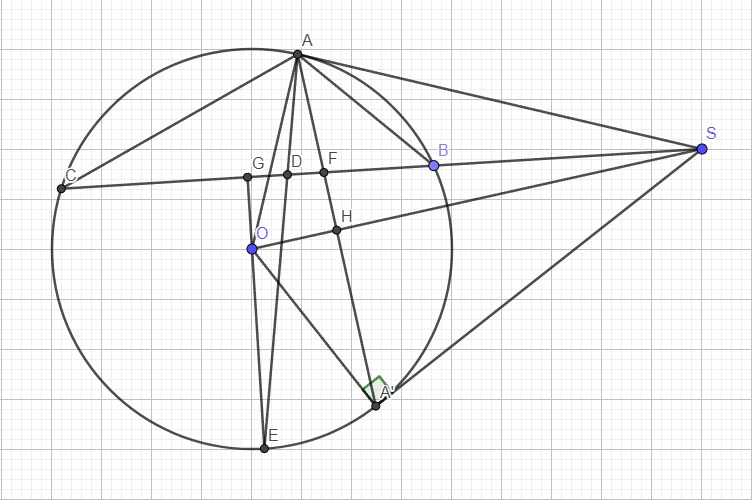
a.
Do AE là phân giác \(\Rightarrow\widehat{BAE}=\widehat{CAE}\Rightarrow sđ\stackrel\frown{BE}=sđ\stackrel\frown{CE}\)
\(\widehat{SAE}\) là góc tạo bởi tiếp tuyến tại A và dây AE \(\Rightarrow\widehat{SAE}=\dfrac{1}{2}sđ\stackrel\frown{AE}\) (1)
\(\widehat{SDA}\) là góc có đỉnh nằm trong đường tròn
\(\Rightarrow\widehat{SDA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{CE}\right)\) \(=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{BE}\right)=\dfrac{1}{2}sđ\stackrel\frown{AE}\) (2)
(1);(2) \(\Rightarrow\widehat{SAE}=\widehat{SDA}\Rightarrow\Delta SAD\) cân tại S
\(\Rightarrow SA=SD\)
b.
Ta có \(SA=SA'\) (t/c hai tiếp tuyến cắt nhau); \(OA=OA'=R\)
\(\Rightarrow SO\) là trung trực của AA'
Hay SO vuông góc AA' tại H hay tam giác SHF vuông tại H
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{CE}\Rightarrow E\) là điểm chính giữa cung BC
OE là đường kính đi qua đi qua điểm chính giữa cung BC \(\Rightarrow OE\perp BC\)
Hay tam giác SGO vuông tại G
Xét hai tam giác SGO và SHF có:
\(\left\{{}\begin{matrix}\widehat{SGO}=\widehat{SHF}=90^0\\\widehat{GSO}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta SGO\sim\Delta SHF\left(g.g\right)\)
\(\Rightarrow\dfrac{SO}{SF}=\dfrac{SG}{SH}\Rightarrow SH.SO=SG.SF\)
c.
SA là tiếp tuyến tại A \(\Rightarrow\Delta SAO\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông SAO với đường cao AH:
\(SA^2=SH.SO\)
Mà theo chứng minh trên \(\left\{{}\begin{matrix}SD=SA\\SH.SO=SG.SF\end{matrix}\right.\)
\(\Rightarrow SD^2=SG.SF\)
d.
Do OE vuông góc BC tại G (theo cm câu b) \(\Rightarrow G\) là trung điểm BC
\(\Rightarrow BG=\dfrac{1}{2}BC=\dfrac{a}{3}\Rightarrow SG=SB+BG=\dfrac{4a}{3}\)
Xét hai tam giác SAB và SCA có:
\(\left\{{}\begin{matrix}\widehat{SAB}=\widehat{SCA}\left(\text{cùng chắn AB}\right)\\\widehat{CSA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta SAB\sim\Delta SCA\left(g.g\right)\)
\(\Rightarrow\dfrac{SA}{SC}=\dfrac{SB}{SA}\Rightarrow SA^2=SB.SC=SB^2.\left(SB+BC\right)=\dfrac{5a^2}{3}\)
Theo đẳng thức câu c: \(SA^2=SD^2=SG.SF\)
\(\Rightarrow SF=\dfrac{SA^2}{SG}=\dfrac{5a}{4}\)