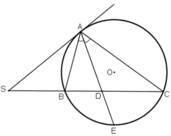
Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
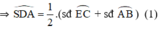
+ 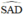 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
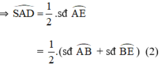
+ 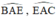 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 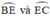
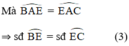
Từ (1); (2) và (3) suy ra 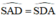
⇒ ΔSAD cân tại S
⇒ SA = SD.

Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
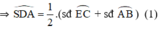
+ 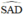 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
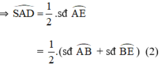
+ 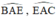 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 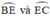
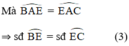
Từ (1); (2) và (3) suy ra 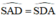
⇒ ΔSAD cân tại S
⇒ SA = SD.
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyển SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn (SB, SC). Tia phân giác của góc BAC cắt dây BC tại D và cắt (O) tại E. a) Chứng minh SA = SD. b) SD2 = SB . SC.
qua điểm S nằm ngoài đường tròn tâm (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn. tia phân giác của góc BAC cắt dây BC tại D. chứng minh SA=SD
Cho đường tròn tâm O và điểm S ở ngoài đường tròn . Từ S kẻ hai tiếp tuyến SA và SD và cát tuyến SBC tới đường tròn ( B ở giữa S và C ).
a) Phân giác của góc BAC cắt dây cung BC ở M . Chứng minh SA = SM .
b) AM cắt đường tròn ở E. Gọi G là giao điểm của OE và BS; F là giao điểm của AD với BC . Chứng minh SA^2 = SG . SF .
c) Biết SB = a ; Tính SF khi BC = \(\dfrac{2a}{3}\)
Mọi người giúp với ạ.
Cho một đường tròn tâm O và một điểm S nằm ngoài đường tròn. Vẽ tiếp tuyến SA và cát tuyến SBC ( B nằm giữa ). Phân giác của góc BAC cắt BC tại D. Chứng minh :
a, SA2= SB.SC
b, SA=SD
c, Trong tất cả các cát tuyến từ S thì cát tuyến qua tâm O là dài nhất.
d. Cho SA = 20, SC = 50. Tính R (O).
Ai biết thì giải dùm với. Cảm ơn nhiều.
Cho (O) và điểm S nằm bên ngoài đường tròn. Từ S vẽ 2 tiếp tuyến SA và SA' và cát tuyến SBC. tia phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Gọi H là giao điểm của OS và AA', G và F lần lượt là giao điểm của OE và AA' với BC
CMR: SA=SB
Cho đường tròn tâm O và điểm S ở ngoài đường tròn . Từ S kẻ hai tiếp
tuyến SA và SD và cát tuyến SBC tới đường tròn (B ở giữa S và C). Phân giác
của góc BAC cắt dây cung BC ở M. SO cắt AD tại H.
a) Chứng minh SO vuông góc với AD
b) Chứng minh SA = SM
c) AM cắt đường tròn ở E. Gọi G là giao điểm của OE và BC, F là giao điểm
của AD với BC .
Chứng minh SA2 = SG . SF
d) Biết SB = a ; Tính SF khi BC = 2a/3
CHo tam giác ABC có 3 góc nhọn, AB < AC nội tiếp đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại S
a) Chứng minh SA2 = SB.SC
b) Tia phân giác của BAC cắt dây và cung nhỏ BC tại D và E. Chứng minh: SA = SD
c) Vẽ đường cao AH của tam giác ABC. CHứng tỏ: OE vuông góc BC và AE là tia phân giác của góc HAO