Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
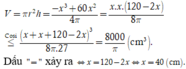
Chọn C.
Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
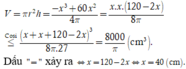
Chọn C.
Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90(cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu để tạo thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là
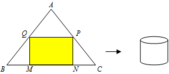
A. 91125 2 π c m 3
B. 13500 3 π c m 3
C. 108000 3 π c m 3
D. 91125 4 π c m 3
Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90(cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu (với M, N thuộc cạnh BC, P và Q tương ứng thuộc cạnh AC và AB) để tạo thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là
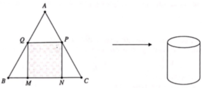
A. 91125 4 π c m 3
B. 91125 2 π c m 3
C. 13500 3 π c m 3
D. 108000 π c m 3
Một miếng tôn hình chữ nhật có chiều dài 10,2 dm, chiều rộng 2π dm được uốn lại thành mặt xung quanh của một chiếc thùng đựng nước có chiều cao 2π dm (như hình vẽ). Biết rằng chỗ ghép mất 2 cm. Biết rằng chỗ ghép mất 2 cm. Hỏi thùng đựng được bao nhiêu lít nước?
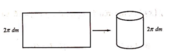
A. 50 lít
B. 100 lí
C. 20,4 lít.
D. 20 lít.
Một miếng tôn hình chữ nhật có chiều dài 10,2 dm , chiều rộng 2 π dm được uốn lại thành mặt xung quanh của một chiếc thùng đựng nước có chiều cao 2 π dm (như hình vẽ). Biết rằng chỗ ghép mất 2 cm. Hỏi thùng đựng được bao nhiêu lít nước?

A. 20 lít.
B. 50 lít.
C. 100 lít
D. 20,4 lít.
Từ một tấm tôn có kích thước 1mx2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)
– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tính tỷ số V 1 V 2 .
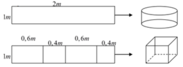
A. V 1 V 2 = 1 0 , 24 π
B. V 1 V 2 = 1 0 , 27 π
C. V 1 V 2 = 1 0 , 7 π
D. V 1 V 2 = 1 0 , 2 π
Người ta cần cắt một tấm tôn có hình dạng là một elip với độ dài trục lớn bằng 2a, độ dài trục bé bằng 2 b a > b > 0 để được một tấm tôn hình chữ nhật nội tiếp elip. Người ta gò tấm tôn hình chữ nhật thu được một hình trụ không có đáy (như hình bên). Tính thể tích lớn nhất có thể thu được của khối trụ đó.
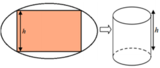
A. 2 a 2 b 3 2 π
B. 2 a 2 b 3 3 π
C. 4 a 2 b 3 2 π
D. 4 a 2 b 3 3 π
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách
- Cách 1. Làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2. Làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật.
( xem hình minh họa dưới đây)
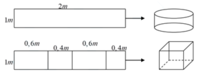
Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tỷ số V 1 V 2 bằng
A. 1 0 , 24 π
B. 1 0 , 27 π
C. 1 0 , 7 π
D. 1 0 , 2 π
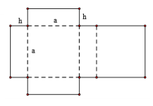
Một bạn đã cắt tấm bìa carton phẳng và cứng có kích thước như hình vẽ. Sau đó bạn ấy gấp theo đường nét đứt thành một hình hộp chữ nhật. Hình hộp có đáy là hình vuông cạnh a (cm), chiều cao là h (cm) và diện tích tấm bìa là 3 m 2 . Tổng a + h bằng bao nhiêu để thể tích hộp là lớn nhất
A. 2 2
B. 2 2
C. 46,3
D. 2
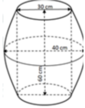
Một thùng đựng bia hơi (có dạng khối tròn xoay như hình vẽ) có đường kính đáy là 30 cm, đường kính lớn nhất của thân thùng là 40 cm, chiều cao thùng là 60 cm, các cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng bia hơi gần nhất với kết quả nào dưới đây? (giả sử độ dày thùng bia không đáng kể)
A. 70 (lít).
B. 62 (lít).
C. 60 (lít).
D. 64 (lít).