Gọi M là trung điểm một cạnh đáy. Khi đó h = S O = S M 2 - O M 2
= 5 - x 2 2 - x 2 4 = 1 2 25 - 10 x = 5 2 5 - 2 x
Theo đề
h = 5 2 ⇔ 5 2 5 - 2 x = 5 2 ⇔ 5 - 2 x = 1 ⇔ x = 2
Đáp án B
Gọi M là trung điểm một cạnh đáy. Khi đó h = S O = S M 2 - O M 2
= 5 - x 2 2 - x 2 4 = 1 2 25 - 10 x = 5 2 5 - 2 x
Theo đề
h = 5 2 ⇔ 5 2 5 - 2 x = 5 2 ⇔ 5 - 2 x = 1 ⇔ x = 2
Đáp án B
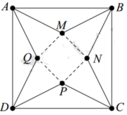
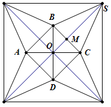
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
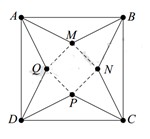
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
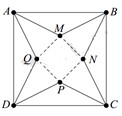
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
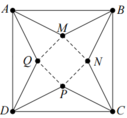
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác bằng nhau là A M B , B N C , C P D và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Cho một tấm nhôm hình vuông cạnh 1(m) như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x(m) Tìm giá trị của x để khối chóp nhận được có thể tích lớn nhất.
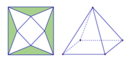
A. x = 2 4
B. x = 2 3
C. x = 2 2 5
D. x = 1 2
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
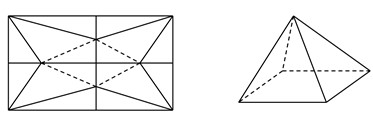
A. x=4
B. x=2
C. x=1
D. x=3
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
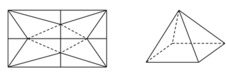
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
Một tấm nhôm hình vuông cạnh 10cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
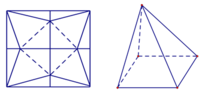
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
A. 2 5
B. 2 5
C. 1
D. 4 5