Các câu hỏi tương tự
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BCa) Chứng minh OA vuông góc với BC tại Hb) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.ADAH.AOc) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm...
Đọc tiếp
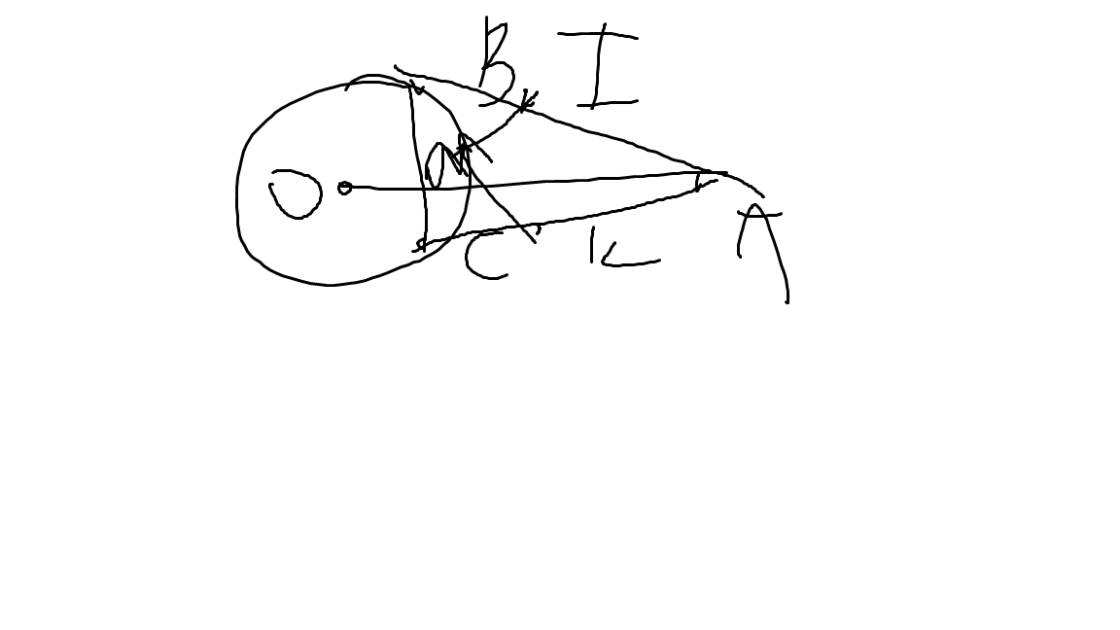
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC
a) Chứng minh OA vuông góc với BC tại H
b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD=AH.AO
c) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm (O)
d) Gọi I là trung điểm cạnh AB, qua I vẽ đừng thẳng vuông góc với cạnh AO tại M và đường thẳng này cắt đường thẳng DF tại N. Chứng minh: ND=NA
1.Từ điểm A ở ngoài đtròn (O) vẽ 2 tiếp tuyến AB và AC với đường tròn(O). Gọi M là trung điểm AB. Nối CM cắt đường tròn(O) tại E. AO cắt BC tại H. Tia AE cắt đường tròn (O) tại Da. Chứng Minh MB bìnhME.MC và CD//ABb. Vẽ OK vuông góc với ED tại K. Vẽ dây cung EN vuông góc với CK (N thuộc (O)). Cm B,O,N thẳng hàng2.Cho điểm M nằm ngoài đtròn (O). Vẽ 2 tiếp tuyến MA,MB với đtròn. Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D), OM cắt A...
Đọc tiếp
1.Từ điểm A ở ngoài đtròn (O) vẽ 2 tiếp tuyến AB và AC với đường tròn(O). Gọi M là trung điểm AB. Nối CM cắt đường tròn(O) tại E. AO cắt BC tại H. Tia AE cắt đường tròn (O) tại D
a. Chứng Minh MB bình=ME.MC và CD//AB
b. Vẽ OK vuông góc với ED tại K. Vẽ dây cung EN vuông góc với CK (N thuộc (O)). Cm B,O,N thẳng hàng
2.Cho điểm M nằm ngoài đtròn (O). Vẽ 2 tiếp tuyến MA,MB với đtròn. Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D), OM cắt AB và (O) lần lượt tại H và I.
a. Cm tg MAOB nội tiếp
b. Cm OH.OM+MC.MD=MO bình
c. Cm CI là tia pg của góc MCH
3. Từ điểm M nằm ngoài (O;R), vẽ 2 tiếp tuyến MA,MB và cát tuyến MCD với (O) (A,B là tiếp điểm và cát tuyến MCD nằm trong góc AMO, MC<MD). Gọi H là giao điểm của AB và OM
a) Cm tg MAOB nội tiếp, OM vuông góc AB
b) Cm AC.BD=AD.BC
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O) .Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H giao điểm của OA và BC.a, Chứng minh OA vuông góc với BC tại Hb. Từ B vẽ đường kính BD của (O). đường thẳng AD cắt (O) tại E ( khác D).Chứng minh AE.AD AH. AOc.Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của (O).
Đọc tiếp
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O) .Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H giao điểm của OA và BC.
a, Chứng minh OA vuông góc với BC tại H
b. Từ B vẽ đường kính BD của (O). đường thẳng AD cắt (O) tại E ( khác D).Chứng minh AE.AD = AH. AO
c.Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của (O).
Lấy điểm A trên (O;R),vẽ tiếp tuyến Ax . Trên Ax lấy điểm B ,trên (O;R) lấy điểm C sao cho BC=AB
a, CMR : CB là tiếp tuyến của (O)
b, Vẽ đường kính AD của (O),kẻ CK vuông góc với AD.
c,Lấy M trên cung nhỏ AC của (O) ,vẽ tiếp tuyến tại M cắt AB,AC lần lượt tại E,F.Vẽ đường tròn tâm I nội tiếp tam giác BFE.CMR:tam giác MAC đồng dạng vs tam giác IFE
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.a, cho biết R5cm, OM3cm. Tính độ dài dây EH.b, Chứng minh AH là tiếp tuyến đường tròn(O)c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tu...
Đọc tiếp
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.
a, cho biết R=5cm, OM=3cm. Tính độ dài dây EH.
b, Chứng minh AH là tiếp tuyến đường tròn(O)
c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.
d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tuyến thứ 2 với đường tròn(O), cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh AE=DQ
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE. a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được. b) Cm: Tích OI.OA không phụ thuộc vào vị trí của điểm A. c) Tia DH cắt OB tại G. Cm: HE ⊥ OC...
Đọc tiếp
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA < 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE.
a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được.
b) Cm: Tích OI.OA không phụ thuộc vào vị trí của điểm A.
c) Tia DH cắt OB tại G. Cm: HE ⊥ OC và EH, OC cắt nhau tại một điểm thuộc IG.
d) OI cắt BC tại M, EM cắt OC tại N. Cm NA là tiếp tuyến của đường tròn ngoại tiếp tam giác ACI.
e) Cm: AN, MD, OB đồng quy tại một điểm.
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE. a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được. b) Cm: Tích OI.OA không phụ thuộc vào vị trí của điểm A. c) Tia DH cắt OB tại G. Cm: HE ⊥ OC...
Đọc tiếp
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA < 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE.
a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được.
b) Cm: Tích OI.OA không phụ thuộc vào vị trí của điểm A.
c) Tia DH cắt OB tại G. Cm: HE ⊥ OC và EH, OC cắt nhau tại một điểm thuộc IG.
d) OI cắt BC tại M, EM cắt OC tại N. Cm NA là tiếp tuyến của đường tròn ngoại tiếp tam giác ACI.
e) Cm: AN, MD, OB đồng quy tại một điểm.
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE. a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được. b) Cm: OI.OA không đổi. c) Tia DH cắt OB tại G. Cm: HE ⊥ OC và GI, EH, OC đồng quy. d) OI cắt BC...
Đọc tiếp
Cho (O) có bán kính R không đổi. Từ một điểm A tùy ý ở ngoài (O) sao cho OA < 2R, vẽ tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi giao điểm của OA và BC là H, lấy điểm D thuộc cung nhỏ BC sao cho HD song song với AB. Vẽ cát tuyến ADE của (O). I là trung điểm của DE.
a) Cm: 5 điểm A, B, C, O, I cùng thuộc một đường tròn, tứ giác DHOE nội tiếp được.
b) Cm: OI.OA không đổi.
c) Tia DH cắt OB tại G. Cm: HE ⊥ OC và GI, EH, OC đồng quy.
d) OI cắt BC tại M, EM cắt OC tại N. Cm NA là tiếp tuyến của đường tròn ngoại tiếp tam giác ACI.
e) Cm: AN, MD, OB đồng quy tại một điểm.
Từ M ngoài đường tròn (O ; 3cm) vẽ các tiếp tuyến MA, MB (A,B là các tiếp điểm). Vẽ đường kính AC , tiếp tuyến tại C của đường tròn (O) cắt AB tại D. MO cắt AB tại I.
1, Tính AB×AD
2, Chứng minh OD vuông góc với MC