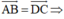 tứ giác ABCD là hình bình hành
tứ giác ABCD là hình bình hành
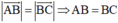
⇒ tứ giác ABCD là hình thoi.
(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)
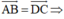 tứ giác ABCD là hình bình hành
tứ giác ABCD là hình bình hành
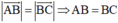
⇒ tứ giác ABCD là hình thoi.
(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)
Câu 1: Trong mặt phẳng 0xy cho A(2;4) B=(-1;4) C=(-5;1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. . ( -8;1 ) B. . ( 6;7) C. . (-2; 1) D. .( 8;1)
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. D( -8; 5).
B. D( 5; 8).
C. D( 8; 5).
D. D( 8; -5).
Trong mặt phẳng oxy cho 3 điểm A(-5;2) B(4:-3) C(6:1) tìm tọa độ D để tứ giác abcd là hình bình hành
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A (3;2) , B(-4;2) ,C (3;5) tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
Cho △ABC biết A (-1;1), B (2;1), C (-1;-3)
a) Tính chu vi tam giác
b) Tìm tọa độ trọng tâm G của tam giác ABC
c) Xác định điểm D sao cho tứ giác ABCD là hình bình hành
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông
Gọi S là diện tích của tứ giác ABCD có độ dài các cạnh là a,b,c,d. CMR: \(S\le\frac{a^2+b^2+c^2+d^2}{2}\)
Trong mặt phẳng Oxy, cho tam giác ABC với A(1;1), B(3;5) và C(5;-1)
a) tìm tọa độ trọng tâm G và tính chu vi của Tam giác ABC
b) tìm tọa độ điểm D để tứ giác ABCD là hình thang với đáy lớn BC và
BC = 2AD