a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 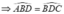 Þ ĐPCM
Þ ĐPCM
a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 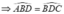 Þ ĐPCM
Þ ĐPCM
Cho hình thang ABCD ( A B / / C D ) có A B = A D = C D / 2 . Gọi M là trung điểm của CD.a) Chứng minh tứ giác ABMD là hình thoi.b) gọi Ac cắt BM tại E, AM cắt BD tại O, N là trung điểm của MC. Chứng minh DOEN là hình thang cân
Cho hbh ABCD có AD=2AB,góc A=60 độ. Gọi E và F lần lượt là trung điểm của BC và AD.
a) c/m AE vuông góc với BF
b) c/m tứ giác BFDC là hình thang cân
c) lấy điểm M đối xứng vơsi A qua B. C/m tứ giác BMCD là hình chữ nhật
d) c/m M,E,D thẳng hàng
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' +BB' +CC' +DD')
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' BB' CC' DD')
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào của hình thang ABCD; Gọi A', B', C’, D’, G' lần lượt là hình chiếu của A, B, C, D, G lên đường thẳng m. Chứng minh GG' = 0.5(AA'+BB'+CC'+DD’)
Bài 1: Cho tứ giác ABCD có độ dài các cạnh là a, b, c, d và có diện tích là S. Chứng mình ABCD là hình vuông khi
a + b + c + d = 4\(\sqrt{S}\)
Bài 2: Cho hình thang ABCD (AB song song CD). Một đường thẳng song song với 2 đáy cắt AD và BC thứ tự ở M và N. Cho biết AB = a, CD = b, \(\frac{MA}{MD}=\frac{m}{n}\), a, b, c, d > 0. Tính M, N theo a, b, m, n.
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
II. Bài tập tự luận
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Giúp mình với Cho tứ giác ABCD có A=D B+C=180 Gọi M N theo thứ tự là trung điểm của BC và AD a chứng minh ABCD là hình thang vuông b chứng minh AM=DM c cho AB=3cm AD=4cm BC=5cm Tính MN
toán hình 8; bài 1; cho hình bình hành ABCD có AD=2*AB, ^A=60độ. gọi E,F lần lượt là trung điểm của BC và AD. c/m;a) c/m AE vuông góc Với BF; b) c/m; BFDC là hình thang cân; c) tính góc ADB; d) lấy M đối xứng với A qua B. c/m tứ giác BMCD là hình chữ nhật,suy ra M,E,D thẳng hàng
Cho tứ giác ABCD, có: góc D < góc C < góc B < góc A và góc C - góc D = góc B - góc C = góc A - góc B. Chứng minh rằng tứ giác ABCD là hình thang