Các câu hỏi tương tự
Cho tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O, góc ABD=góc ACD. gọi E là giao điểm của 2 đường thẳng AD và BC
a,tam giác AOB đồng dạng với tam giác DOC
b,tam giác AOD đồng dạng với tam giác BOC
c,EA.ED=ED.EC
tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, góc ABD= góc ACD. Gọi E là giao điểm của AD và BC. Chứng minh:
a) Tam giác AOB đồng dạng với tam giác DOC.
b) Tam giác AOD đồng dạng với tam giác BOC.
c)EA.ED=EB.EC
tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O, góc ABD = góc ACD.
Gọi I là giao điểm của 2 đường thẳng AD và BC.
CMR 1/ Tg AOB đồng dạng với Tg DOC
b/ tam giác AOD đồng dạng vs tam giác BOC.
c/ AI.ID=IB.IC
cho tứ giác ABCD có các góc đối bù nhau. Gọi O là giao điểm 2 đường chéo AC và Bd, E là giao điểm hai cạnh AD và BC.
a, cmr: AE.CD= EC.AB và tam giác EAC đồng dạng tam giác EBC
b,cmr: góc ABD= góc dca
giup minh voi
Cho tứ giác ABCD, AC cắt BD tại O, biết góc ABD = góc ACD. Gọi M là giao điểm của 2 đg thẳng AB và BC.
CMR: a) Tam giác AOB đồng dạng tam giác BOC
b) Tam giác AOD đồng dạng tam giác BOC
c) MA. MD = MB. MC
Cho tứ giác ABCD, gócABDgócACB, AB giao với BD tại O.
a) Chứng minh: tam giác AOD đồng dạng tam giác BOC.
b) Chưng minh tam giác AOB đồng dạng tam giác DOC
c) Gọi E là giao của AB và CD. Chứng minh EA.EBED.EC
Đọc tiếp
Cho tứ giác ABCD, gócABD=gócACB, AB giao với BD tại O.
a) Chứng minh: tam giác AOD đồng dạng tam giác BOC.
b) Chưng minh tam giác AOB đồng dạng tam giác DOC
c) Gọi E là giao của AB và CD. Chứng minh EA.EB=ED.EC
Cho tứ giác ABCD, gócABDgócACB, AB giao với BD tại O.
a) Chứng minh: tam giác AOD đồng dạng tam giác BOC.
b) Chưng minh tam giác AOB đồng dạng tam giác DOC
c) Gọi E là giao của AB và CD. Chứng minh EA.EBED.EC
Đọc tiếp
Cho tứ giác ABCD, gócABD=gócACB, AB giao với BD tại O.
a) Chứng minh: tam giác AOD đồng dạng tam giác BOC.
b) Chưng minh tam giác AOB đồng dạng tam giác DOC
c) Gọi E là giao của AB và CD. Chứng minh EA.EB=ED.EC
Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O,
∠
(ABD)
∠
(ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:
△
AOB đồng dạng
△
DOC
Đọc tiếp
Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, ∠ (ABD) = ∠ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: △ AOB đồng dạng △ DOC
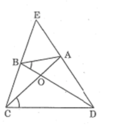
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại I và góc ABD= góc ACD
a, Chứng minh tam giác AIB đồng dạng với tam giác DIC
b,AI.BC=AD.BI
c, Từ D kẻ tia phân giác DM của tam giác ADC. Tính DM biết AC=5cm, AD=3cm và góc ADC=90 độ









