a, Chứng minh được P A 2 = P C . P B và P A 2 = P O 2 = O A 2 => tính được PO
b, Chứng minh được D B C ^ = D A B ^ = 1 2 C A B ^ => ĐPCM
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
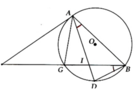
từ điểm P ở ngoài đường tròn (O), vẽ hai tiếp tuyến PA và PB. qua B kẻ Bx song song với PA cắt đường tròn (O) tại C. gọi E là giao điểm thứ hai của PC với (O) và I là giao điểm của BE với PA
a. chứng minh tứ giác PAOB nội tiếp
b. chứng minh PA2=PE.PC
c. chứng minh IP=IA
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE2. Cho tứ giác ABCD có AB BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh: a) tứ giác AQRC nội tiếp được 1 đường tròn b) QR//AD
Đọc tiếp
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Từ điểm P ở ngoài đường tròn tâm O vẽ hai tiếp tuyến PA và PB . Qua B kẻ Bx song song với AP , nó cắt đường tròn tâm O ở C. Gọi D là giao điểm thứ hai của PC với đường tròn. Gọi E là giao điểm của BD và AP.
a, chứng minh tam giác PEB đồng dạng với tam giác DEP.
b, chứng minh PE = EA
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm (O). Từ B và C vẽ hai tiếp tuyến của đường tròn, hai tiếp tuyến này cắt nhau ở D. Qua D vẽ một cát tuyến sonng song với AB, cát tuyến này cắt đường tròn tại các điểm M và N và cắt cạnh AC tai I
a) Chứng minh tứ giác OBDC nội tiếp đường tròn (O)
b) Chứng minh I là trung điểm của dây MN
từ điểm P ngoài (O<R) vẽ hai tiếp tuyến PA và PB đến (O,R) vơus A,B là các tiếp điểm . Gọi H là chân đường vuông góc vẽ từ A đến đường kính BC của đường tròn .AC cắt BP tainh D , CP cắt AH tại I
1) Chứng minh : tam giác APD cân và P là trung điểm của BD
2) chứng minh : I là trung điểm của AH
Từ điểm P ở ngoài đường tròn (O) vẽ tiếp tuyến PA (A là tiếp điểm). Gọi B là trung điểm của PA, vẽ cát tuyến BCD với đường tròn. PC và PD giao với đường tròn lần lượt tại E và F. Chứng minh : AP // EF.
Cho đường tròn 0 và một điểm P ở ngoài đường tròn. Kẻ 2 tiếp tuyến PA, PB với đường tròn O( A,B là tiếp điểm) PO cắt đường tròn tại K và I ( K nằm giữa P và (O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).a, C/m tứ giác BHCP nội tiếpb, C/m AC vuông góc CHc, Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. C/m M là trung điểm AQd, giả sử góc BDC 45 độ tính diện tích tam giác PBD phần nằm ngoài đường tròn O theo R
Đọc tiếp
Cho đường tròn 0 và một điểm P ở ngoài đường tròn. Kẻ 2 tiếp tuyến PA, PB với đường tròn O( A,B là tiếp điểm) PO cắt đường tròn tại K và I ( K nằm giữa P và (O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).
a, C/m tứ giác BHCP nội tiếp
b, C/m AC vuông góc CH
c, Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. C/m M là trung điểm AQ
d, giả sử góc BDC = 45 độ tính diện tích tam giác PBD phần nằm ngoài đường tròn O theo R
Từ điểm P ở bên ngoài đường tròn (O) ,vẽ tiếp tuyến PA và PB tới đường tròn ( A và B là 2 tiếp điểm ).Qua P kẻ tia Bx//PA cắt đường tròn ( O ) tại C.Gọi E là giao điểm của PC với đường tròn ( O ).Và F là giao điểm của BE với PA.Chứng minh: a)AF2=FE.FB b)F là trung điểm của AP c)AE.BC=AC.PE d)AE.BC+AC.BE=AB.EC
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (vói F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Cho biết AF
4
R
3
a, Chứng minh tứ giác OBDF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác nàyb, Tính côsin góc
D
A
B...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (vói F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Cho biết AF = 4 R 3
a, Chứng minh tứ giác OBDF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác này
b, Tính côsin góc D A B ^
c, Kẻ OM ^ BC (M Î AD). Chứng minh
B
D
D
M
-
D
M
A
M
=
1
d, Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R