Chọn D.
Phương pháp: Sử dụng tích phân.
Cách giải: Diện tích phần gạch chéo là

Vậy m=3 thỏa mãn yêu cầu bài toán.
Chọn D.

Phương pháp: Sử dụng tích phân.
Cách giải: Diện tích phần gạch chéo là

Vậy m=3 thỏa mãn yêu cầu bài toán.
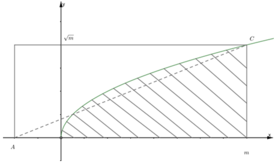
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A(-1;0) và C(a; a ), với a> 0. Biết rằng đồ thị hàm số y= x chia hình (H) thành hai phần có diện tích bằng nhau. Tìm a
A. a= 9
B. a= 4
C. a= 1/2
D. a= 3
Trong mặt phẳng tọa độ, cho hình chữ nhật H có một cạnh nằm trên trục hoành và có hai đỉnh trên một đường chéo là A - 1 ; 0 và C a ; a với a > 0. Biết rằng đồ thị hàm số y = x chia hình H thành hai phần có diện tích bằng nhau, tìm a
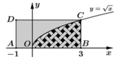
A. a = 1 2
B. a = 3
C. a = 4
D. a = 9
Cho hàm số y = x 2 - m x ( 0 < m < 4 ) có đồ thị (C). Gọi S 1 là diện tích hình phẳng giới hạn bởi (C) và trục hoành; S 2 là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x=m,x=4. Biết S 1 = S 2 , giá trị của m bằng
A. 10 3 .
B. 2.
C. 3.
D. 8 3 .
Gọi (H) là hình phẳng giới hạn bởi đồ thị (P) của hàm số y = 6 x - x 2 và trục hoành. Hai đường thẳng y = m , y = n chia hình (H) thành ba phần có diện tích bằng nhau. Tính P = 9 - m 3 + 9 - n 3
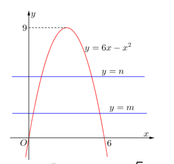
A. P = 405
B. P = 409
C. P = 407
D. P = 403
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = − x 2 + 4 x và trục hoành. Hai đường thẳng y = m và y = n chia H thành 3 phần có diện tích bằng nhau (tham khảo hình vẽ). Giá trị biểu thức T = 4 − m 3 + 4 − n 3 bằng
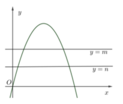
A. T = 320 9 .
B. T = 75 2 .
C. T = 512 15 .
D. T = 405 .
Biết rằng hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x - m (m là tham số thực) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao nhiêu?
A. m = ± 1
B. m = ± 2
C. m = 2
D. m = 1
Biết rằng hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x − m (m là tham số thực) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao nhiêu ?
A. m = ± 1
B. m = ± 2
C. m = 2
D. m = 1