Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, AB a, BC 2a. Hai tia Bx và Cy cùng vuông góc với mặt phẳng (ABC) và nằm cùng một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B,C sao cho BB a, CC 2a. Tính cosin góc giữa hai mặt phẳng (ABC) và (ABC). A.
30
10
B.
15
10
C.
14
10
D. ...
Đọc tiếp
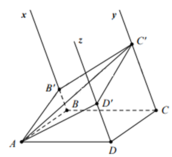
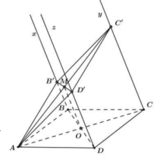
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mặt phẳng (ABC) và nằm cùng một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B',C' sao cho BB' = a, CC' = 2a. Tính cosin góc giữa hai mặt phẳng (ABC) và (A'B'C').
A. 30 10
B. 15 10
C. 14 10
D. 42 14
Trong không gian Oxyz, cho mặt phẳng
(
α
)
:
2
x
+
y
-
2
z
-
2
0
, đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A(1/2; 1; 1). Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng Oxy tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 / 3
B. 7 / 2
C. 21 / 2
D. 3 / 2
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
y
-
2
z
-
2
0
, đường thẳng
d
:
x
+
1
2
y
+
2
2
z
+...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 2 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 2
B. 21 2
C. 7 3
D. 3 2
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với A(1;2;1), B(–2;1;3), C(2;–1;1), D(0;3;1). Viết phương trình mặt phẳng (P) chứa hai điểm A, B sao cho C, D nằm về hai phía khác nhau của (P) đồng thời C, D cách đều (P)
A. (P) : 2x + 3z – 5 = 0
B. P) : 4x + 2y + 7z – 15 = 0
C. (P) : 3y + z – 1 = 0
D. (P) : x – y + z – 5 = 0
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với
A
(
1
;
2
;
1
)
,
B
(
–
2
;
1
;
3
)
,
C
(
2
;
–
1
;
1
)
,
D
(
0
;
3
;
1
)
.
Viết phương...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với A ( 1 ; 2 ; 1 ) , B ( – 2 ; 1 ; 3 ) , C ( 2 ; – 1 ; 1 ) , D ( 0 ; 3 ; 1 ) . Viết phương trình mặt phẳng (P) chứa hai điểm A, B sao cho C, D nằm về hai phía khác nhau của (P) đồng thời C, D cách đều (P)
A. ( P ) : 2 x + 3 z – 5 = 0
B. ( P ) : 4 x + 2 y + 7 z – 15 = 0
C. ( P ) : 3 y + z – 1 = 0
D. ( P ) : x – y + z – 5 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 2x+y-2z-2 0 và đường thẳng có phương trình
d
:
x
+
a
1
y
+
2
2
z
+
3
2
và điểm A(1/2;1;1) Gọi ∆ là đường thẳng nằm trong mặt phẳng (α) , song song vớ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 2x+y-2z-2 = 0 và đường thẳng có phương trình d : x + a 1 = y + 2 2 = z + 3 2 và điểm A(1/2;1;1) Gọi ∆ là đường thẳng nằm trong mặt phẳng (α) , song song với d, đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/3
B. 7/2
C. 21 2
D. 3/2
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
y
−
2
z
−
2
0
,
đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + y − 2 z − 2 = 0 , đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Trong không gian Oxyz , cho mặt phẳng
P
:
x
+
y
-
z
-
4
0
và điểm
A
2
,
-
1
,
3
.
Gọi D là đường thẳng đi qua A và song song với (P) , biết D có một vectơ chỉ phương là
u
→
a...
Đọc tiếp
Trong không gian Oxyz , cho mặt phẳng P : x + y - z - 4 = 0 và điểm A 2 , - 1 , 3 . Gọi D là đường thẳng đi qua A và song song với (P) , biết D có một vectơ chỉ phương là u → a , b , c , đồng thời D đồng phẳng và không song song với Oz . Tính a c
A. -1/2
B. 1/2
C. 2
D. – 2
Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;2;1),B(-2;1;3),C(2;-1;3),D(0;3;1). Mặt phẳng (P):ax+by+cz-20=0 đi qua hai điểm A,B và cách đều hai điểm C,D và hai điểm C,D nằm về cùng một phía so với mặt phẳng (P). Tính S=a+b+c.
A. S = 7
B. S = 15
C. S = 6
D. S = 13