Đáp án C
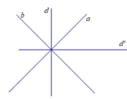
Hình có 2 trục đối xứng, đó là các đường thẳng a, d’, a và b
Trong đó a và b là các đường phân giác của các góc tạo bởi 2 đường thẳng d và d’
Đáp án C

Hình có 2 trục đối xứng, đó là các đường thẳng a, d’, a và b
Trong đó a và b là các đường phân giác của các góc tạo bởi 2 đường thẳng d và d’
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 3 x − y + 2 = 0 . Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng trục Oy
A. 3 x ' + y ' − 2 = 0
B. 3 x ' − y ' − 2 = 0
C. 3 x ' + y ' + 2 = 0
D. − 3 x ' + y ' − 2 = 0
Trong mặt phẳng Oxy, cho đường thẳng d: x-2y+2=0; d': x-2y-8=0. Phép đối xứng tâm biến d thành d' và biến trục Ox thành chính nó có tâm I là
A. I(0;-3)
B. I(0;3)
C. I(-3;0)
D. I(3;0)
Trong mặt phẳng tọa độ Oxy, cho điểm C(2; -5) và đường thẳng D:3x-4y+4=0. Trên đường thẳng D hai điểm A và B đối xứng nhau qua điểm I 2 ; 5 2 sao cho diện tích tam giác ABC bằng 15. Tìm tọa độ điểm A biết điểm B có hoành độ dương.
A. A(8; 7)
B. A(4; 4)
C. A(0; 1)
D. A(-4; -2
Trong mặt phẳng tọa độ Oxy cho đường thằng d có phương trình 2y+x+3=0. Phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục Ox là
A. y-2x+3=0.
B. -2y+x+3=0.
C. 2y+x-3=0.
D. 2y-x+3=0.
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình y = 1 3 x + 2 .Viết phương trình đường thẳng Δ là ảnh của đường thẳng d qua phép đối xứng trục là đường thẳng y=x.
A. y = 3 x − 6
B. y = 3 x + 6
C. y = − 3 x + 6
D. y = − 3 x − 6
Cho hình vuông ABCD cạnh a tâm O. Dựng đường thẳng D qua O và vuông góc với mặt phẳng (ABCD). Trên đường thẳng lấy hai điểm S và S’ đối xứng nhau qua O sao cho SA = S’A = a. Cosin góc giữa hai mặt phẳng (SAB) và (S’AB) bằng:
A. 4 9
B. 0
C. 1 3
D. - 1 3
Trong mặt phẳng tọa độ Oxy, xác định giá trị của tham số m để hai đường thẳng d : 2 x - 3 y + 4 = 0 và d ' x = 2 - 3 t y = 1 - 4 m t vuông góc với nhau
A. 9 8
B. 1 2
C. - 9 8
D. - 1 2
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d cắt hai trục Ox và Oy lần lượt tại 2 điểm A(a;0) và B 0 ; b a ≠ 0 , b ≠ 0 . Viết phương trình đường thẳng d.
A. d : x a + y b = 0
B. d : x a − y b = 1
C. d : x a + y b = 1
D. d : x b + y a = 0
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A 0 ; 2 ; 4 , B 1 ; 2 ; − 3 và mặt phẳng P : x + y + z = 0 . Xét đường thẳng d thay đổi thuộc (P) và đi qua B, gọi H là hình chiếu vuông góc của A trên d. Biết rằng khi d thay đổi thì H thuộc một đường tròn cố định. Bán kính R của đường tròn đó là:
A. R = 38 2 .
B. R = 3 2 .
C. R = 1 2 .
D. R = 3 3 2 .