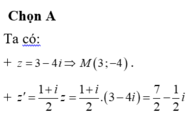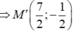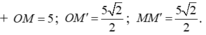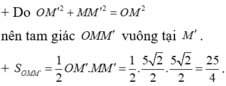Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức
z
1
-
2
i
, N là điểm biểu diễn số phức
z
¯
1
-
i
2
z
. Tính diện tích tam giác OMM′.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức z = 1 - 2 i , N là điểm biểu diễn số phức z ' ¯ = 1 - i 2 z . Tính diện tích tam giác OMM′.
![]()
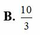
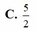
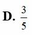
Cho số phức z=25/(3+4i). Điểm biểu diễn hình học số phức liên hợp của z trong mặt phẳng Oxy là
A.M(3;-4)
B.N(2;-3)
C.P(3;-2)
D.Q(3;4)
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức
z
1
2
-
i
,
z
2
1
+
4
i
Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
Đọc tiếp
Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức z 1 = 2 - i , z 2 = 1 + 4 i Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
![]()
![]()
![]()
![]()
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và
i
+
1
z
. Tính z biết diện tích tam giác OAB bằng 8.
Đọc tiếp
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và i + 1 z . Tính z biết diện tích tam giác OAB bằng 8.
![]()
![]()
![]()
![]()
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z. Tính
z
biết diện tích tam giác OAB bằng 8. A.
z
2
2
B.
z
4
2
C.
z...
Đọc tiếp
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính z biết diện tích tam giác OAB bằng 8.
A. z = 2 2
B. z = 4 2
C. z = 2
D. z = 4
Trong mặt phẳng Oxy gọi A,B,C lần lượt là các điểm biểu diễn số phức z1=-3i,z2=2-2i,z3=-5-i. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức
A. z=-1-i
B.z=-1-2i
C.z=1-2i
D.z=2-i
Cho các số phức z13-2i, z21+4i và z3-1+i có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng: A.. B.12. C.. D.9.
Đọc tiếp
Cho các số phức z1=3-2i, z2=1+4i và z3=-1+i có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:
A.![]() .
.
B.12.
C.![]() .
.
D.9.
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w 2z + 1 - i là hình tròn có diện tích A. S 9π. B. S 12π. C. S 16π. D. S 25π.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích
A. S = 9π.
B. S = 12π.
C. S = 16π.
D. S = 25π.
Tìm tọa độ điểm M trong mặt phẳng Oxy là điểm biểu diễn số phức z3-4i. A. B. C. .
Đọc tiếp
Tìm tọa độ điểm M trong mặt phẳng Oxy là điểm biểu diễn số phức z=3-4i.
A.![]()
B.![]()
C.![]()
.![]()