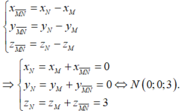Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;1), B(-1;-2;0), C(2;0;-1). Tập hợp các điểm M cách đều ba điểm A,B,C là đường thẳng
△
. Viết phương trình đường thẳng
△
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;1), B(-1;-2;0), C(2;0;-1). Tập hợp các điểm M cách đều ba điểm A,B,C là đường thẳng △ . Viết phương trình đường thẳng △ .
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0;3;-2) và N(2;-1;0). Tọa độ của véc tơ
M
N
→
là: A. (2;-4;2) B. (1;1;-1) C. (-2;4;-2) D. (2;2;-2)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0;3;-2) và N(2;-1;0). Tọa độ của véc tơ M N → là:
A. (2;-4;2)
B. (1;1;-1)
C. (-2;4;-2)
D. (2;2;-2)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là A.
x
3
+
y
-
2
+
z
2
-
1
B.
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là
A. x 3 + y - 2 + z 2 = - 1
B. x 3 + y - 2 + z 2 = 0
C. x 3 + y 2 + z - 2 = 1
D. x 3 + y - 2 + z 2 = 1
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là A.
x
3
+
y
-
2
+
z
2
-
1
B. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là
A. x 3 + y - 2 + z 2 = - 1
B. x 3 + y - 2 + z 2 = 0
C. x 3 + y 2 + z - 2 = 1
D. x 3 + y - 2 + z 2 = 1
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến
n
→
của mặt phẳng A.
n
→
(1;-1;1) B.
n
→
(1;1;-1) C. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến n → của mặt phẳng
A. n → =(1;-1;1)
B. n → =(1;1;-1)
C. n → =(2;-1;1)
D. n → =(2;1;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3), N(2;3;1) và P(3;-1;2). Tọa độ điểm Q sao cho MNPQ là hình bình hành là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3), N(2;3;1) và P(3;-1;2). Tọa độ điểm Q sao cho MNPQ là hình bình hành là:
![]()
![]()
![]()
![]()
Trong hệ trục tọa độ Oxyz, cho các điểm M(1;-1;1), N(2;0;-1), P(-1;2;1). Xét điểm Q sao cho tứ giác MNPQ là một hình bình hành. Tọa độ Q là
Đọc tiếp
Trong hệ trục tọa độ Oxyz, cho các điểm M(1;-1;1), N(2;0;-1), P(-1;2;1). Xét điểm Q sao cho tứ giác MNPQ là một hình bình hành. Tọa độ Q là
![]()
![]()
![]()
![]()
Trong không gian tọa độ
O
;
i
→
,
j
→
,
k
→
, cho ba vecto
a
→
1
;
2
;
3
,...
Đọc tiếp
Trong không gian tọa độ O ; i → , j → , k → , cho ba vecto a → = 1 ; 2 ; 3 , b → = - 2 ; 0 ; 1 , c → = - 1 ; 0 ; 1 . Tìm tọa độ của vecto n → = a → + b → + 2 c → - 3 i →
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;2), B(0;-1;1), C(2;-1;0). Điểm M thỏa mãn
3
M
A
→
+
4
M
B
→
−
M
C
→
0
→
thì điểm M có tọa độ là A.
M
−
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;2), B(0;-1;1), C(2;-1;0). Điểm M thỏa mãn 3 M A → + 4 M B → − M C → = 0 → thì điểm M có tọa độ là
A. M − 5 6 ; 1 2 ; 5 3
B. M − 5 6 ; − 1 2 ; 5 3
C. M 5 6 ; − 1 2 ; 5 3
D. M − 5 6 ; − 1 2 ; − 5 3