Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là A.
x
3
+
y
-
2
+
z
2
-
1
B.
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là
A. x 3 + y - 2 + z 2 = - 1
B. x 3 + y - 2 + z 2 = 0
C. x 3 + y 2 + z - 2 = 1
D. x 3 + y - 2 + z 2 = 1
Trong không gian với hệ toạ độ Oxyz, cho 3 điểm M(3;0;0), N(0;-2;0), P(0;0;1). Mặt phẳng (MNP) có phương trình:
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho 3 điểm M(3;0;0), N(0;-2;0), P(0;0;1). Mặt phẳng (MNP) có phương trình:
![]()
![]()
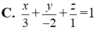
![]()
Trong không gian với hệ tọa độ Oxyz cho A(-3;0;0), B(0;0;3), C(0;-3;0) và mặt phẳng (P): x+y+z -3 0. Tìm trên (P) điểm M sao cho
M
A
→
+
M
B
→
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A(-3;0;0), B(0;0;3), C(0;-3;0) và mặt phẳng (P): x+y+z -3 =0. Tìm trên (P) điểm M sao cho M A → + M B → - M C → nhỏ nhất
A. M(3;3;-3)
B. M(-3;-3;3)
C. M(3;-3;3)
D. M(-3;3;3)
Trong không gian với hệ tọa độ Oxyz , cho A(−3;0;0), B(0;0;3), C(0; −3;0) và mặt phẳng (P):
x
+
y
+
z
-
3
0
. Tìm trên (P) điểm M sao cho
M
A
¯
+
M
B
¯
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho A(−3;0;0), B(0;0;3), C(0; −3;0) và mặt phẳng (P): x + y + z - 3 = 0 . Tìm trên (P) điểm M sao cho M A ¯ + M B ¯ + M C ¯ nhỏ nhất.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;3;0) và mặt phẳng (P): x + y + z - 3 0. Tìm trên (P) điểm M sao cho
M
A
→
+
M
B
→
-
M
C
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho M A → + M B → - M C → nhỏ nhất.
A. M (3;3;-3)
B. M (-3;-3;3)
C. M (3;-3;3)
D. M (-3;3;3)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-70 và đường thẳng
d
:
x
-
3
-
2
y
+
8
4
z
-
1
. Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-7=0 và đường thẳng d : x - 3 - 2 = y + 8 4 = z - 1 . Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng: (P): x + y + z - 2 0 (Q): x + 2y - z +3 0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,
cho hai mặt phẳng:
(P): x + y + z - 2 = 0
(Q): x + 2y - z +3 = 0
và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P)
và (Q).
![]()
![]()
![]()
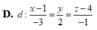
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x - y + z + 3 0 và ba điểm A(0;1;2), B(1;1;1), C(2;-2;3) Tọa độ điểm M thuộc (P) sao cho
M
A
→
+
M
B
→
+
M
C
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x - y + z + 3 = 0 và ba điểm A(0;1;2), B(1;1;1), C(2;-2;3) Tọa độ điểm M thuộc (P) sao cho M A → + M B → + M C → nhỏ nhất là
A. M(0;0;−3)
B. M(1;1;−3)
C. M(−1;2;0)
D. M(2;1;−1)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B((-3;-2;0) và mặt phẳng (P):x+3y-z+20. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B((-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là:
![]()
![]()
![]()
![]()



