Đường thẳng ∆ đi qua A(1;1;0) có VTCP

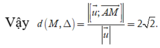
Chọn C.
Cách 2. Tìm tọa độ hình chiếu H của M trên ∆ . Khi đó d(M, ∆ ) = MH
Đường thẳng ∆ đi qua A(1;1;0) có VTCP

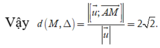
Chọn C.
Cách 2. Tìm tọa độ hình chiếu H của M trên ∆ . Khi đó d(M, ∆ ) = MH
Trong không gian với hệ tọa độ Oxyz, cho điểm M 1 2 ; 3 ; 1 và đường thẳng ∆ : x + 2 1 = y - 1 2 = z + 2 - 2 . Tính khoảng cách d từ điểm M 1 đến đường thẳng ∆
A. d = 10 2 3
B. d = 10 3 3
C. d = 10 5 3
D. d = 10 3
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;1;1) và đường thẳng d : x - 1 1 = y - 2 2 = z - 3 - 2 . Tính khoảng cách từ A đến đường thẳng d
A. 3 5 2
B. 2 5
C. 5
D. 3 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z - 10 = 0 điểm A(1;3;2) và đường thẳng d : x = - 2 + 2 t y = 1 + t z = 1 - t . Tìm phương trình đường thẳng D cắt (P) và d lần lượt tại hai điểm M và N sao cho A là trung điểm của cạnh MN
A. x - 6 7 = y - 1 - 4 = z + 3 - 1
B. x + 6 7 = y + 1 4 = z - 3 - 1
C. x - 6 7 = y - 1 4 = z + 3 - 1
D. x + 6 7 = y + 1 - 4 = z - 3 - 1
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d): x - 2 2 = y + 2 - 1 = z - 3 1 . Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đến mặt phẳng ( α ): 2x+2y-z-1=0 là:
A. 2
B. 2 3
C. 1 3
D. 1
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A - 2 ; 1 ; 0 , B 4 ; 4 ; - 3 , C 2 ; 3 ; - 2 và đường thẳng d : x - 1 1 = y - 1 - 2 = z - 1 - 1 . Gọi α là mặt phẳng chứa d sao cho A, B, C ở cùng phía đối với mặt phẳng α . Gọi d 1 , d 2 , d 3 lần lượt là khoảng cách từ A, B, C đến α . Tìm giá trị lớn nhất của T = d 1 + 2 d 2 + 3 d 3 .
A. T m a x = 2 21
B. T m a x = 6 14
C. T m a x = 14 + 203 3 + 3 21
D. T m a x = 203
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình x − 1 2 = y − 3 = z − 2 0 và mặt phẳng P : x + y = 0 . Tìm tọa độ điểm M trên d có hoành độ dương sao cho khoảng cách từ M đến (P) bằng 2 .
A. M 3 ; − 3 ; 2
B. M 7 ; − 9 ; 2
C. M 5 ; − 6 ; 2
D. M − 1 ; 3 ; 2
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình x − 1 1 = y + 1 2 = z − 2 − 1 và mặt phẳng P : x + 2 y − 2 z + 4 = 0 . Tìm tọa độ điểm M trên d có tung độ dương sao cho khoảng cách từ M đến (P) bằng 2.
A. M 3 ; 3 ; 0
B. M 2 ; 1 ; 1
C. M 0 ; - 3 ; 3
D. M 1 ; - 1 ; 2
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 1 2 = z - 1 1 ; d 2 : x 1 = y + 1 2 = z - 6 - 5 . gọi A là giao điểm của d 1 v à d 2 ; d là đường thẳng qua điểm M (2; 3;1) cắt d 1 , d 2 lần lượt tại B, C sao cho B C = 6 A B . Tính khoảng cách từ O đến đường thẳng d, biết rằng d không song song với mặt phẳng (Oxz)
A. 10 5
B. 10 3
C. 13
D. 10
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3 2 = y + 2 1 = z + 1 - 1 và mặt phẳng (P): x + y + z + 2 = 0. Đường thẳng ∆ nằm trong mặt phẳng (P), vuông góc với đường thẳng d đồng thời khoảng cách từ giao điểm I của d với (P) đến ∆ bằng 42 . Gọi M(5;b;c) là hình chiếu vuông góc của I trên ∆. Giá trị của bc bằng
A. - 10
B. 10
C. 12
D. - 20