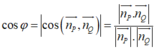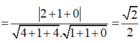Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình
P
:
x
−
y
+
4
z
−
2
0
và
Q
:
2
x
−
2
z
+
7
0
. Góc giữa hai mặt phẳng (P) và (Q) là A.
90
°
B.
45
°
C.
60
°
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình P : x − y + 4 z − 2 = 0 và Q : 2 x − 2 z + 7 = 0 . Góc giữa hai mặt phẳng (P) và (Q) là
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P): x + (m+1)y – 2z + m 0 và (Q): 2x – y +3 0 với m là tham số thực. Để mặt phẳng (P) và (Q) vuông góc thì giá trị của m bằng bao nhiêu? A. m -5 B. m 1 C. m 3 D. m -1
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P): x + (m+1)y – 2z + m = 0 và (Q): 2x – y +3 = 0 với m là tham số thực. Để mặt phẳng (P) và (Q) vuông góc thì giá trị của m bằng bao nhiêu?
A. m = -5
B. m = 1
C. m = 3
D. m = -1
Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng (P)=x+(m+1)y-2z+m=0 và (Q): 2x-y+3=0, với m là tham số thực. Để (P) và (Q) vuông góc thì giá trị của m bằng bao nhiêu?
A. m=-5
B. m=1
C. m=3
D. m=-1
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x+(m+1)y-2z+m0 và (Q): 2x-y+30 với m là tham số thực. Để (P) và (Q) vuông góc thì giá trị của m bằng bao nhiêu A. -5 B. 1 C. 3 D. -1
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x+(m+1)y-2z+m=0 và (Q): 2x-y+3=0 với m là tham số thực. Để (P) và (Q) vuông góc thì giá trị của m bằng bao nhiêu
A. -5
B. 1
C. 3
D. -1
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) : x+(m+1)y-2z+m=0 và (Q) 2x-y+3=0, với m là tham số thực. Để (P) (Q) vuông góc thì m bằng bao nhiêu
A. m=-5
B. m=1
C. m=3
D. m=-1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y - z - 1 0 và điểm A(1;0;0)
∈
(P). Đường thẳng
∆
đi qua A nằm trong mặt phẳng (P) và tạo với trục Oz một góc nhỏ nhất. Gọi
M
(
x
0
;
y
0
;
z
0
)
là giao điể...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y - z - 1 = 0 và điểm A(1;0;0) ∈ (P). Đường thẳng ∆ đi qua A nằm trong mặt phẳng (P) và tạo với trục Oz một góc nhỏ nhất. Gọi M ( x 0 ; y 0 ; z 0 ) là giao điểm của đường thẳng ∆ với mặt phẳng (Q): 2x + y - 2z + 1 =0. Tổng bằng S = x 0 + y 0 + z 0
A. -5
B. 12
C. -2
D. 13
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) :
2
x
+
m
2
x
-
2
z
+
1
0
và (Q)
m
2
x
-
y
+
m
2
-
2
z
+
2
0
. Tìm tất cả các giá trị để (P)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) : 2 x + m 2 x - 2 z + 1 = 0 và (Q) m 2 x - y + m 2 - 2 z + 2 = 0 . Tìm tất cả các giá trị để (P) (Q) vuông góc
A. m ≥ 3
B. m = 2
C. m = 2
D. m = 1
Trong không gian với hệ tọa độ Oxyz, điểm nào trong các điểm sau đây thuộc cả hai mặt phẳng (P): x-3y-z+40 và (Q): 2x-y+2z-50 ?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, điểm nào trong các điểm sau đây thuộc cả hai mặt phẳng (P): x-3y-z+4=0 và (Q): 2x-y+2z-5=0 ?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) : x+y-z+1=0 và (Q) -2x+my+2z-2=0. Tìm m để (P) // (Q)
A. m=-2
B. m=5
C. Không tồn tại m
D. m=2