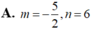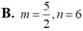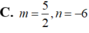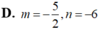Đáp án C
Phương pháp:
Mặt phẳng
![]()
![]()
Cách giải: Mặt phẳng (P):2x-3y+z-2018=0 có 1 VTPT là n → =(2;-3;1)
Đáp án C
Phương pháp:
Mặt phẳng
![]()
![]()
Cách giải: Mặt phẳng (P):2x-3y+z-2018=0 có 1 VTPT là n → =(2;-3;1)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;5), B(1;-2;3). Mặt phẳng α đi qua hai điểm A,B và song song với trục Ox có vect ơ pháp tuyến n → ( 0 ; a ; b ) . Khi đó , tỷ số a b bằng
A. 2
B. -2
C. - 3 2
D. 3 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - z + 1 = 0 . Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng α : 2 x + 4 y − 5 z + 2 = 0 , β : x + 2 y − 2 z + 1 = 0 và γ : 4 x − m y + z + n = 0 . Để ba mặt phẳng đó có chung giao tuyến thì tổng m+n bằng
A. -4
B. 8
C.-8
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B((-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng qua A(-1;1;-2) và có véc tơ pháp tuyến n → = 1 ; - 2 ; - 2 là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, mặt phẳng mx+ny+2z+1=0 có một vec tơ pháp tuyến là n → ( 3 ; 2 ; 1 ) khi:
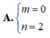
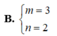
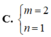
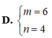
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+3y-4z+5=0. Vecto nào sau đây là 1 vecto pháp tuyến của mặt phẳng (P)?
A. (-4;3;2)
B. (2;3;-4)
C. (2;3;4)
D. (2;3;5)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình -2x + 2y -z -3 = 0. Mặt phẳng (P) có một vectơ pháp tuyến là:
A. (-2;2;-3)
B. (4;-4;2)
C. (-4;4;2)
D. (0;0;-3)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 2x + y – z + 3 = 0 và đường thẳng d : x = 2 + m t y = n + 3 t z = 1 - 2 t . Với giá trị nào của m, n thì đường thẳng d nằm trong mặt phẳng (P)?