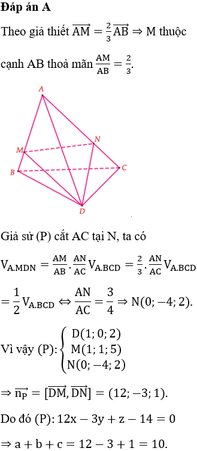
Các câu hỏi tương tự
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;0;0),B(0;2;0),C(0;0;3). Mặt phẳng qua hai điểm B,C và tâm mặt cầu nội tiếp tứ diện OABC là ax+by+cz-6=0. Giá trị của biểu thức a+b+c bằng
A. -4.
B. -18.
C. 4.
D. 18.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;0;0),B(0;-2;0),C(0;0;-2). Các điểm M, N, P lần lượt trên ba cạnh OA, OB, OC sao cho
O
A
O
M
+
O
B
O
N
+
O
C
O
P
4...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;0;0),B(0;-2;0),C(0;0;-2). Các điểm M, N, P lần lượt trên ba cạnh OA, OB, OC sao cho O A O M + O B O N + O C O P = 4 và khối tứ diện OMNP có thể tích nhỏ nhất. Mặt phẳng ( α ) :ax+by+cz-1=0 đi qua ba điểm M, N, P. Tính S=a+b+c.
A. S = - 9 2
B. S = -4
C. S = -2
D. S = -3
Trong không gian với hệ tọa độ Oxyz, mặt phẳng
(
P
)
:
a
x
+
b
y
+
c
z
+
d
0
,
a
2
+
b
2
+
c
2
0
đi qua điểm B(1;0;2) , C(-1;-1;0) và cách A(2;5;3) một khoảng lớn nhất. Khi đó g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng ( P ) : a x + b y + c z + d = 0 , a 2 + b 2 + c 2 > 0 đi qua điểm B(1;0;2) , C(-1;-1;0) và cách A(2;5;3) một khoảng lớn nhất. Khi đó giá trị của biểu thức M = a + c b + d là
A. M = 1
B. M = 3 4
C. M = - 2 7
D. M = - 3 2
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm
A
(
a
;
1
;
−
2
)
,
B
(
1
;
0
;
−
1
)
,
C
(
2
;
−
1
;
3
)
,
D
(
1
;
0
;
2
)
. Biết thể tích của tứ diện AB...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A ( a ; 1 ; − 2 ) , B ( 1 ; 0 ; − 1 ) , C ( 2 ; − 1 ; 3 ) , D ( 1 ; 0 ; 2 ) . Biết thể tích của tứ diện ABCD bằng 1 và điểm A có hoành dương. Khi đó giá trị a bằng
A. a = 1
B. a = 3
C. a = 2
D. = 4
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3
2
16
và các điểm A(1;0;2), B(-1;2;2)....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 16 và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) và mặt cầu (S ) có diện tích nhỏ nhất. Khi đó viết phương trình (P):ax + by + cz + 3 = 0. Tính giá trị của T = a + b + c.
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
−
2
2
+
z
−
3
2
16
và các điểm
A...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 16 và các điểm A 1 ; 0 ; 2 , B − 1 ; 2 ; 2 . Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+3=0. Tính tổng T=a+b+c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3
2
16
và các điểm A(1;0;2), B(-1;2;2)....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 16 và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+3=0. Tính tổng T=a+b+c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-1;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là: A. D(0;-3;-1) B. D(0;1;-1) C. D(0;2;-1) D. D(0;3;-1)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-1;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là:
A. D(0;-3;-1)
B. D(0;1;-1)
C. D(0;2;-1)
D. D(0;3;-1)
Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;2;1),B(-2;1;3),C(2;-1;3),D(0;3;1). Mặt phẳng (P):ax+by+cz-20=0 đi qua hai điểm A,B và cách đều hai điểm C,D và hai điểm C,D nằm về cùng một phía so với mặt phẳng (P). Tính S=a+b+c.
A. S = 7
B. S = 15
C. S = 6
D. S = 13