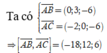 là một VTPT của mp (ABC)
là một VTPT của mp (ABC)
![]() nên mp (SBH) có một VTPT là
nên mp (SBH) có một VTPT là ![]()
Vậy mp (SBH) đi qua điểm B(0;3;0) và có một VTPT ![]()
nên có phương trình x + 5y - 7z - 15 = 0. Chọn A.
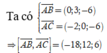 là một VTPT của mp (ABC)
là một VTPT của mp (ABC)
![]() nên mp (SBH) có một VTPT là
nên mp (SBH) có một VTPT là ![]()
Vậy mp (SBH) đi qua điểm B(0;3;0) và có một VTPT ![]()
nên có phương trình x + 5y - 7z - 15 = 0. Chọn A.
Trong không gian với hệ trục tọa độ Oxyz, phương trình tham số của đường thẳng d đi qua điểm A(1;2;3) và vuông góc với mặt phẳng (α):4x+3y-7z+1=0 là:
A. d : x = 4 + t y = 3 + 2 t z = - 7 + 3 t
B. d : x = 1 + 8 t y = - 2 + 6 t z = 3 - 14 t
C. d : x = 1 + 3 t y = 2 - 4 t z = 3 - 7 t
D. d : x = 1 + 4 t y = 2 + 3 t z = 3 - 7 t
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) , trong đó a > 0 , b > 0 , c > 0 và 3 a + 1 b + 3 c = 5 . Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 , khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?
A . ( 0 ; 1 2 ) .
B. (0;1).
C. (1;3).
D. (4;5).
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng α : 4 x - 3 y - 7 z + 3 = 0 và điểm I(1;-1;2). Phương trình mặt phẳng đối xứng với α qua I là
A. β : 4x - 3y - 7z - 3 = 0
B. β : 4x - 3y - 7z + 11 = 0
C. β : 4x - 3y - 7z - 11 = 0
D. β : 4x - 3y - 7z + 5 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 mặt phẳng α : x + 4 y + z - 11 = 0 . Gọi (P) là mặt phẳng vuông góc với (a), (P) song song với giá của véctơ v → = 1 ; 6 ; 2 và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P).
A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0
B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0
C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0
D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + y − z − 2 = 0 và đường thẳng d : x + 1 2 = y − 1 1 = z − 2 1 . Phương trình nào dưới đây là phương trình mặt phẳng chứa đường thẳng (d) và vuông góc với mặt phẳng α
A. x + y − z + 2 = 0
B. 2 x − 3 y − z + 7 = 0
C. x + y + 2 z − 4 = 0
D. 2 x − 3 y − z − 7 = 0
Trong không gian với hệ tọa độ Oxyz, cho S : x - a 2 + y - b 2 + z 2 - 2 c z = 0 là phương trình mặt cầu, với a, b, c là các số thực và c ≠ 0 . Khẳng định nào sau đây đúng?
A. luôn đi qua gốc tọa độ
B. (S) tiếp xúc với mặt phẳng O
C. (S) tiếp xúc với trục Oz
D. (S) tiếp xúc với các mặt phẳng (Oyz) và (Ozx)
Trong không gian với hệ tọa độ Oxyz, cho S : x - a 2 + y - b 2 + z 2 - 2 c z = 0 là phương trình mặt cầu, với a,b,c là các số thực và c ≠ 0 . Khẳng định nào sau đây đúng?
A. (S) luôn đi qua gốc tọa độ O.
B. (S) tiếp xúc với mặt phẳng (Oxy).
C. (S) tiếp xúc với trục Oz.
D. (S) tiếp xúc với các mặt phẳng (Oyz) và (Ozx) .
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x + 6 y − 4 z − 2 = 0 , mặt phẳng α : x + 4 y + z − 11 = 0. Gọi (P) là mặt phẳng vuông góc với α , P song song với giá của vecto v → 1 ; 6 ; 2 v à P tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2 x − y + 2 z − 2 = 0 và x − 2 y + z − 21 = 0
B. x − 2 y + 2 z + 3 = 0 và x − 2 y + z − 21 = 0
C. 2 x − y + 2 z + 3 = 0 và 2 x − y + 2 z − 21 = 0
D. 2 x − y + 2 z + 5 = 0 và x − 2 y + 2 z − 2 = 0
Trong không gian với hệ tọa độ Oxyz, phương trình ( α ) mặt phẳng A ( 0 ; − 1 ; 0 ) , B ( 2 ; 0 ; 0 ) ; C ( 0 ; 0 ; 3 ) đi qua điểm là
A. x 2 + y 1 + z 3 = 1.
B. x 2 + y − 1 + z 3 = 0.
C. x − 1 + y 2 + z 3 = 1.
D. x 2 + y − 1 + z 3 = 1.