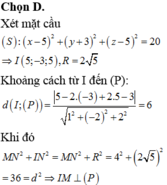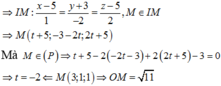Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
−
2
y
+
2
z
−
3
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
−
10
x
+
6
y
−
10
z
+
39...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x − 2 y + 2 z − 3 = 0 và mặt cầu S : x 2 + y 2 + z 2 − 10 x + 6 y − 10 z + 39 = 0 . Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với(S) tại N. Biết MN = 4. Tính độ dài đoạn OM.
A. O M = 6
B. OM = 3.
C. OM = 5.
D. O M = 11
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng
P
:
x
−
y
+
z
0
và mặt cầu (S) có tâm
I
1
;
−
1
;
1
và bán kính R 3. Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu S tại điểm N. Tính khoảng cách từ M tới gốc tọa độ biết rằng MN...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P : x − y + z = 0 và mặt cầu (S) có tâm I 1 ; − 1 ; 1 và bán kính R = 3. Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu S tại điểm N. Tính khoảng cách từ M tới gốc tọa độ biết rằng MN = 4.
A. 19
B. 2 2
C. 22
D. 5
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng
P
:
x
-
2
y
+
2
z
-
3
0
và mặt cầu (S) có tâm I(5;-3;5) bán kính
R
2
5
. Từ một điểm A thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu (S) tại điểm B. Tính OA biết rằng AB 4. A. OA 3 B. OA
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P : x - 2 y + 2 z - 3 = 0 và mặt cầu (S) có tâm I(5;-3;5) bán kính R = 2 5 . Từ một điểm A thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu (S) tại điểm B. Tính OA biết rằng AB = 4.
A. OA = 3
B. OA = 11
C. OA = 6
D. OA = 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
-
2
y
+
2
z
-
3
0
và mặt cầu (S) có tâm I(5;-3;5), bán kính
R
2
5
. Từ một điểm A thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu (S) tại điểm B. Tính OA biết rằng AB 4 A. OA 3 B.
O
A
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x - 2 y + 2 z - 3 = 0 và mặt cầu (S) có tâm I(5;-3;5), bán kính R = 2 5 . Từ một điểm A thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu (S) tại điểm B. Tính OA biết rằng AB = 4
A. OA = 3
B. O A = 11
C. O A = 6
D. OA = 5
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+150 và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
2
x
-
y
+
2
z
-
14
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
+
2
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - y + 2 z - 14 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Tìm điểm M thuộc (S) sao cho khoảng cách từ M tới (P) lớn nhất.
A. M=(-1;-1''-3)
B. M=(1;-1;-3)
C. M=(-1;1;-3)
D. M=(-1;-1;3)
Trong không gian Oxyz, cho mặt phẳng
P
:
2
x
-
y
+
2
z
-
14
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
+
2
z
-
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng
P : 2 x - y + 2 z - 14 = 0 và mặt cầu
S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Gọi tọa độ điểm M (a; b; c) thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất. Tính giá trị biểu thức K = a + b + c.
A. K = -2.
B. K = -5.
C. K = 2.
D. K = 1.
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
và mặt phẳng
P
:
2
x
+
2
y
-
2
z
+
15...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 và mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 . Khoảng cách ngắn nhất giữa điểm (M) trên (S) và điểm N trên (P) bằng
A. 3 3 2
B. 3 2 3
C. 3 2
D. 2 3
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P):
2
x
-
2
y
-
z
+
1
0
, (Q):
x
+
2
y
-
2
z
-
4
0
....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2