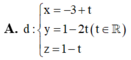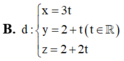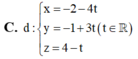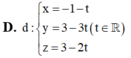Đáp án B
1 2 A B → =(1;2;-1) là vectơ pháp tuyến của mặt phẳng trung trực của AB. I(2;1;0) là trung điểm của AB, khi đó phương trình mặt phẳng trung trực của đoạn AB là x-2+2(y-1)-z=0
<=> x+2y-z-4=0
Đáp án B
1 2 A B → =(1;2;-1) là vectơ pháp tuyến của mặt phẳng trung trực của AB. I(2;1;0) là trung điểm của AB, khi đó phương trình mặt phẳng trung trực của đoạn AB là x-2+2(y-1)-z=0
<=> x+2y-z-4=0
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;1) mặt phẳng (P):x-2y+z-1=0 và đường thẳng d : x 1 = y - 2 2 = z - 1 - 1 . Viết phương trình đường thẳng đi qua A, song song với mặt phẳng (P) cắt đường thẳng d.
![]()
![]()
![]()
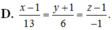
Trong không gian với hệ tọa độ Oxyz,
cho hai mặt phẳng:
(P): x + y + z - 2 = 0
(Q): x + 2y - z +3 = 0
và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P)
và (Q).
![]()
![]()
![]()
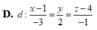
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : x 1 = y - 1 1 = z - 2 1 và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
A . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
B . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
C . S : x + 1 2 + y + 2 2 + z + 3 2 = 5
D . S : x - 1 2 + y - 2 2 + z - 3 2 = 3
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng d đi qua điểm A(1;2;1) và vuông góc với mặt phẳng (P): x-2y+z-1=0 có dạng
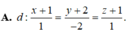
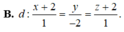
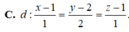
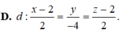
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z - 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 2 3 .Viết phương trình đường thẳng ∆ nằm trong mặt phẳng P đồng thời cắt và vuông góc với đường thẳng d.
![]()
![]()
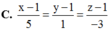
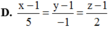
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua hai điểm A(0;1;0), B(2;3;1) và vuông góc với mặt phẳng (Q):x+2y-z=0 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 2 1 = y - 2 1 = z - 1 và mặt phẳng ( P ) : x + 2 y – 3 z + 4 = 0 . Phương trình tham số của đường thẳng d nằm trong (P), cắt và vuông góc đường thẳng ∆ là:
A. x = 1 - 3 t y = - 2 + 3 t z = - 1 + t
B. x = - 3 + 2 t y = 1 - t z = 1 + t
C. x = - 3 - 3 t y = 1 + 2 t z = 1 + t
D. x = - 3 + t y = 1 - 2 t z = 1 - t
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + z – 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 2 3 Viết phương trình đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho đường thẳng ∆ : x 1 = y - 1 1 = z - 2 - 1 và mặt phẳng (P): x+2y+2z-4=0. Phương trình đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với đường thẳng ∆ là