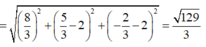Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;2;2), B(2;-2;0). Gọi I 1 ( 1 ; 1 ; - 1 ) và I 2 ( 3 ; 1 ; 1 ) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S).
A. R = 219 3
B. R = 2 2
C. R = 129 3
D. R = 2 6
Đáp án C
Ta có
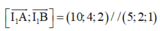
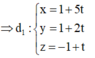
là trục đường tròn tâm I 1 ( 1 ; 1 ; - 1 ) đi qua A, B
Lại có
![]()
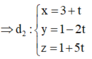
là trục đường tròn tâm I 2 ( 3 ; 1 ; 1 ) đi qua A, B
Tâm mặt cầu (S) chứa cả 2 đường tròn có tâm I ( 8 3 ; 5 3 ; - 2 3 ) là giao điểm của d 1 , d 2
Bán kính mặt cầu cần tìm là R = IA