Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x + 1 2 = y 3 = z + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi M a ; b ; c là giao điểm của d với đường thẳng Δ . Giá trị P = a + b + c bằng
A. -2
B. 4
C. 2
D. 6

- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
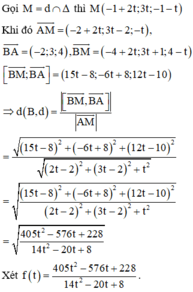
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)




